推荐系统——召回

NOTE

这是 b 站王树森推荐系统课程的笔记，记录到了重排，之后的物品冷启动和提分部分我没有学，所以也没有笔记。索引如下：

• 推荐系统——概述
• 推荐系统——召回
• 推荐系统——排序
• 推荐系统——特征交叉
• 推荐系统——行为序列
• 推荐系统——重排

基于物品的协同过滤 (ItemCF)

原理

1. 认为用户会喜欢相似的物品
2. 喜欢两个物品的用户重叠很大，则两个物品相似

已知物品 $i_{1},i_{2},\dots$，对任意一个用户 $u$ 以及一个新物品 $i$，计算 $u$ 对 $i$ 的兴趣：

其中

• $\text{like}(u,i_{j})$ 通过收藏转发等方式计算
• $\text{sim}(i_{j},i)$：对任意一个物品 $i$，记所有对 $i$ 感兴趣的用户为 $U=\{u_{1},u_{2},\dots\}$，构造对应的向量，每一维放用户对 $i$ 的喜爱分数 $\text{like}(u_{j},i)$，然后对 $i_{j}$ 和 $i$ 计算余弦相似度得到（而不是根据物品内容进行计算）即

其中 $V=U_{1}\cap U_{2}$，不考虑喜欢程度的话：

完整过程

1. 事先做离线计算，建立“用户 -> 物品”索引（最近点击、交互过的物品 ID 及喜爱程度）、“物品 -> 物品”索引（两两之间相似度，每个物品最相似的 $k$ 个物品）
2. 线上召回
   1. 对一个用户，取最近感兴趣的物品列表（$n$ 个）
   2. 对取出的 $n$ 个物品，找到 top-$k$ 相似物品（最多 $n\cdot k$ 个，因为要去重）
   3. 对相似物品进行计算，返回前若干个物品

特点：使用索引，离线计算量大，线上计算量小

Swing 召回通道

1. ItemCF 的问题：如果有一个小圈子，以及两个不相关的物品 $i_{1},i_{2}$，圈子内的两个用户分别将这两个物品转发到圈子内，导致大量用户同时点开了这两个物品，会造成这两个物品的相似度估计不准确
2. Swing 认为两个用户同时感兴趣的物品越多，则越有可能是这样的小圈子里面的人，则应该降低权重

对两个物品 $i_{1},i_{2}$，同上记 $V=U_{1}\cap U_{2}$，对 $V$ 中用户 $u_{1},u_{2}$，重合度记为 $\text{overlap}(u_{1},u_{2})$，由同时感兴趣的物品决定大小，同时感兴趣的物品越多，则 overlap 越大。计算相似度：

基于用户的协同过滤（UserCF）

原理

认为如果两个用户相似，则他们喜欢的物品也应该相似

和 ItemCF 基本一致，但是使用用户之间的相似度替代物品之间的相似度。

先不考虑物品热门程度：

其中 $J=I_{1}\cap I_{2}$。但是一个物品越热门，就越容易被两个人同时喜欢，则这两个人的（平均）相似度就越低，所以需要赋予热门权重，此时

其中 $n_{l}$ 是喜欢物品 $l$ 的人数

完整过程

和 ItemCF 仅有少数替换上的不同，不做赘述。

矩阵补充（Matrix Completion）

将用户、物品都 embedding 之后，计算 embedding 向量的内积，值越大说明越感兴趣。

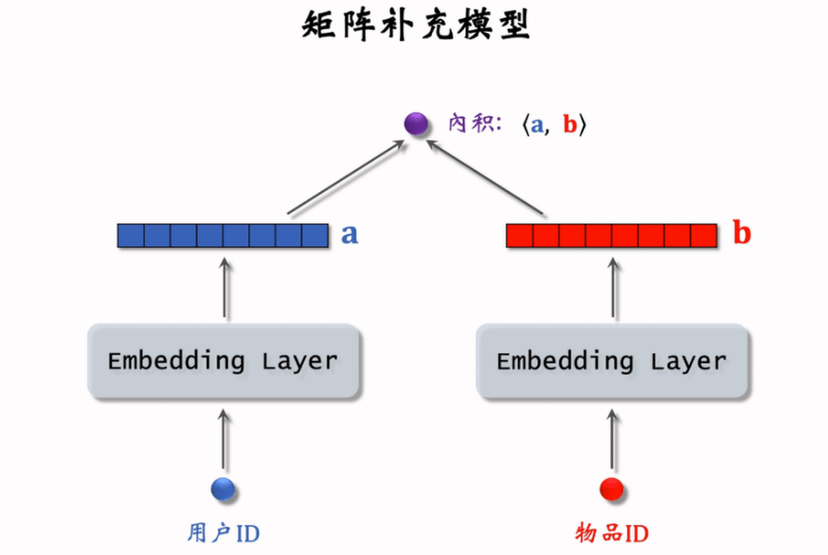
数据集 $\Omega$：（用户，物品，兴趣分数）$(u,i,y)$ 的三元组集合，兴趣分数 $y$ 通过系统指标计算

训练：将 $u$ 号用户映射为向量 $a_{u}$，第 $i$ 号物品映射为向量 $b_{i}$，分别可以组成 embedding 矩阵 $A,B$，求解优化问题：

存储：训练得到的矩阵 $A$ 和 $B$，将 $A$ 的列存储为 key-value 表（用户 ID - embedding 向量）

线上服务：对用户 $u$，通过计算内积选取内积最大的 $k$ 个物品，但是这样时间复杂度和物品数量呈线性关系，在实际中无法 work，可以使用近似最近邻查找（Approximate Nearest Neighbor Search），可以得到比最优结果稍弱的结果

实践中矩阵补充并不能 work，因为

1. 只用了 ID embedding，而没有利用物品、用户属性等信息
2. 负样本的选取方式不对
3. 做训练的方法不好（内积不如余弦相似度，平方损失不如交叉熵损失）

双塔模型

模型

对物品/用户特征的处理：

1. ID：同矩阵补充，embedding 成一个向量
2. 离散特征：要么 embedding（维数过大），要么直接使用 one-hot 编码（维数不大）
3. 连续特征：归一化、log 处理、分桶等

然后将得到的向量拼接之后，送入一个神经网络，输出最终的表征

然后使用余弦相似度计算喜爱程度，和矩阵补充就一样了

训练

1. Pointwise：独立看待每个正负样本，做简单的二元分类（正样本尽可能接近 1，负样本则 -1）
2. Pairwise：每次各取一个正负样本
   1. 鼓励 $\cos(a,b^{+})$ 大于 $\cos(a,b^{-})$，使用 triplet hinge loss：$L(a,b^{+},b^{-})=\max_{}\{ 0,\cos(a,b^{-})+m-\cos(a,b^{+}) \}$，$m$ 为超参数，即希望正样本至少比负样本大 $m$
   2. 也有其他 loss，如 triplet logistic loss：$L(a,b^{+},b^{-})=\log(1+\exp(\sigma \cdot(\cos(a,b^{-})-\cos(a, b^{+}))))$，$\sigma>0$ 为超参
3. Listwise：一个正，多个负
   1. 鼓励 $\cos(a,b^{+})$ 尽可能大，$\cos(a,b_{i}^{-})$ 尽可能小，见下图

正负样本

正样本：曝光且用户点击过的物品。由于热门物品更容易被点击，所以需要过采样冷门物品或者降采样热门物品

负样本：

1. 简单负样本（没有被召回的物品），都需要注意热门/冷门物品的 2-8 效应影响：
   1. 全体样本
   2. batch 内样本（使用 list-wise 方式训练时，会过度打压热门物品，需要纠偏：对用户 $a_{i}$ 和物品 $b_{j}$，$b_{j}$ 被抽样到的概率为 $p_{j}$，训练的时候，将 $\cos(a_{i},b_{j})$ 替换为 $\cos(a_{i},b_{j})-\log p_{j}$，线上召回时不需要替换）
2. 困难负样本
   1. 被粗排淘汰的物品（较困难）
   2. 精排分数后，靠后的物品（非常困难）
3. 错误负样本：曝光但是没有点击的物品，是错误的！这些物品用于排序训练，而不是召回。
   1. 因为召回的目标是“快速找到用户可能感兴趣的物品”，这些错误负样本只能说明用户对别的更感兴趣，或者碰巧没有点击，不应该用于召回训练，但可以用于排序训练。

一般将简单负样本和困难负样本按 50% 来混合，进行训练

召回

1. 在上线前，首先计算物品塔，得到物品的向量并储存在向量数据库中
2. 上线后，对需要的用户，线上计算向量，然后去数据库中检索物品
   1. 因为用户特征时刻在发生变化且变化较快，事先计算存储意义不大，成本也太高；物品的特征相对稳定
   2. 每次召回只使用一个用户向量，但是会涉及到上亿个物品，所以事先计算物品向量并存储

模型更新

• 全量更新：例如在凌晨，使用上一天全天的数据，在上一天的模型参数的基础上继续训练，训一个 epoch。得到新的用户塔和物品向量
• 增量更新：即 online learning，实时收集数据，增量更新 ID embedding 参数（不更新其他部分的参数，工程上的经验），会有一定的延迟，例如十多分钟
  • 注意全量更新的模型不使用增量更新得到的模型，而是使用上一次全量更新后得到的模型
  • 只做增量更新是有偏的，因此需要全量更新，随机打乱一天的数据，消除偏差

双塔模型 + 自监督

双塔模型学不好低曝光物品的表征，引入自监督可以缓解这个问题

特征变换：

1. random mask：随机选择离散特征并 mask 掉
2. dropout：对多值的离散特征
3. 互补特征：将物品的特征进行随机分组，每一组中先随机舍弃一种特征，然后重新舍弃该组的其他特征（即互补特征）。如特征 $\{ a,b,c,d \}$ 划分为两组 $\{ a,b \},\{ c,d \}$，第一次舍弃 $b,d$，第二次舍弃 $a,c$，会得到两个对同一物品的表征，希望能够足够接近
4. mask 一组关联的特征：
   1. 对特征 $u,v$，通过计算互信息来衡量相关性，即 $MI(U,V)=\sum_{u\in U}\sum_{v\in V}p(u,v)\log \frac{p(u,v)}{p(u)p(v)}$
   2. 先离线算出所有特征的互信息矩阵，然后训练时随机选取一个特征，mask 掉和它最相关的若干特征，然后进行训练
   3. 效果比上面三个更好，但是更复杂，不易维护

将不同物品经过相同的几个特征变换，这里假设两个，从物品 $a \to a',a''$ 以及 $b\to b',b''$，那么自然希望 $a'$ 和 $a''$ 相似度尽可能高，而 $a'$ 和 $b',b''$ 相似度尽可能低。具体训练时，对每一个 batch 做两类特征变换，得到样本 $b_{1}',b_{2}',\dots,b_{m}'$ 和 $b_{1}'',b_{2}'',\dots,b_{m}''$，第 $i$ 个物品的损失函数：

也就是和 Listwise 的训练方式类似的损失函数。这个损失将和双塔模型的损失加权得到最终损失

Deep Retrieval

将物品表征为路径，线上查找用户最匹配的路径

首先是路径的定义：想象一个 3 层，每层有 $K$ 个元素 $\{ 1,2,3,\dots K \}$ 的结构，那么一个三元组 $[a,b,c]\in [K]^{3}$ 就是一条路径。

然后是路径和物品之间的映射：

1. 一个物品可以对应多条路径
2. 一条路径对应了一组物品

之后就可以预估用户对路径的兴趣：给定用户特征 $x$，计算 $p(a\mid x)$，然后计算下一层 $p(b\mid a,x)$，以此类推（即链式计算）得到 $p(a,b,c\mid x)$。选择每一层的节点时，可以使用 beam search 的方法。每一次计算都使用一个对应的神经网络。得到最感兴趣的一条路径，就可以取出一组物品了（如果过多，则用一个小的排序模型进行打分后取出需要的数量）。

训练：

1. 只用正样本，即 $\text{clike}(\text{user},\text{item})=1$ 的二元组 $(\text{user},\text{item})$
2. 神经网络：物品表征为 $J$ 条路径，$[a_{1},b_{1},c_{1}],\dots,[a_{J},b_{J},c_{J}]$，损失函数：$-\log \sum_{j=1}^{J}p(a_{j},b_{j},c_{j}\mid x)$
3. 物品表征：对路径 $p=[a,b,c]$ 和物品 $i$，相关度 $\text{score}(p,i)=\sum_{u} p(a,b,c\mid u) \cdot \text{click}(u,i)$，根据这个值选出 $J$ 条路径作为物品的表征（记为集合 $\Pi$）损失函数：$\text{loss}(i,\Pi)=-\log \sum_{j=1}^{J}\text{score}(p_{j},i)$
   1. 为了避免过多物品集中在一条路径上：正则化，取一条路径上的物品数量的四次方

其他召回通道

• 地理位置召回：如 GeoHash 召回/同城召回，对一个区域内的优质笔记，取出最新的若干篇（因为没有个性化，所以需要优质），按新到旧的顺序排序
• 作者召回：关注的作者，或者有交互的作者，相似作者
• 缓存召回：复用前 $n$ 次推荐精排的结果

曝光过滤

看过某个物品，则不再把该物品推荐给该作者（不过有例外，例如长视频平台可以重复推荐相同视频）

对一个用户，看过 $n$ 个物品，本次召回 $r$ 个物品，则暴力对比的话需要 $O(nr)$ 时间，不能接受。

使用 bloom filter 结构：如果判断为 no，则一定不在集合中；反之，则很可能在集合中。具体的：

1. 把物品集合表征为一个 $m$ 维01向量：每个用户的曝光物品的集合（共 $n$ 个物品）表征为 $m$ bit 的向量存储
2. Bloom filter 用 $k$ 个哈希，每个哈希把物品 ID 映射为 0 到 $m-1$ 之间的整数
3. 误判的概率为：$\delta \approx\left( 1-\exp\left( -\frac{kn}{m} \right) \right)^{k}$，最优参数为 $k=1.44\ln\left( \frac{1}{\delta} \right), m=2n\ln\left( \frac{1}{\delta } \right)$

对一个哈希的情况：

而对 $k=3$ 的情况：

总链路：

缺点是不支持删除物品，对时间过久的物品也会记录在案，影响误伤率。需要定期重算。