量子物理笔记

2025-04-21

WARNING
Updating…

前量子力学#

1.1 热辐射黑体辐射#

所有物体在任何温度下都要发射电磁波，这种与温度有关的辐射称为热辐射 (heat radiation)
热辐射波谱是连续谱
平衡热辐射: 加热一物体，若物体所吸收的能量等于在同一时间内辐射的能量，则物体的温度恒定。这种温度不变的热辐射称之为平衡热辐射
单色辐出度 $M_{\lambda}$ ：物体单位表面在单位时间内发出的波长在 $\lambda$ 附近单位波长间隔内的电磁波的能量，为单色辐出度 $M_{\lambda}$

\begin{align*} M_{\lambda}(T)=\frac{\mathrm{d}E_{\lambda}}{\mathrm{d}\lambda } \end{align*}

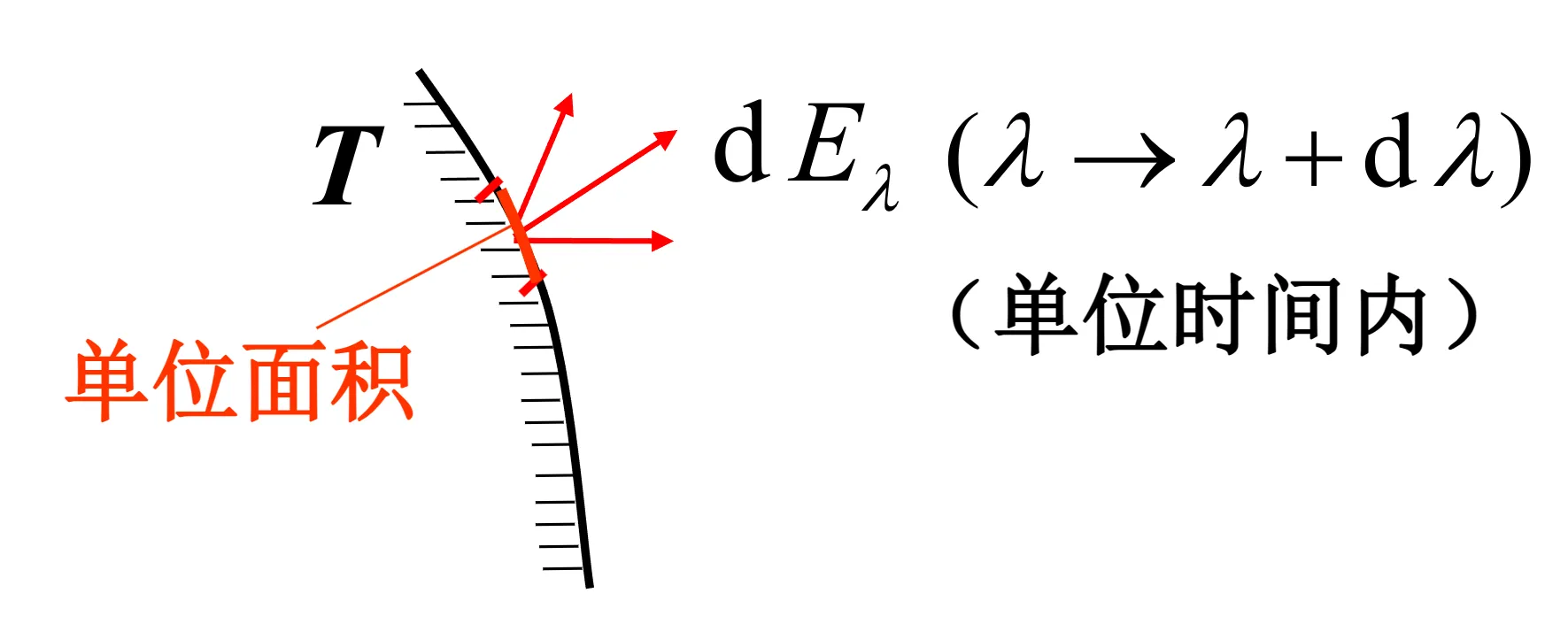
dansefuchudu

辐出度 $M(T)$ ：物体从单位面积上发射的所有各种波长的辐射总功率称为物体的总辐出度 $M(T)$ ，单位 $W / m^{2}$

\begin{align*} M(T)= \int _{0}^{\infty}M_{\lambda}(T) \, \mathrm{d} T \end{align*}

吸收比: 当辐射从外界入射到物体表面时，吸收能量与入射总能量之比

\begin{align*} \alpha(T) = \frac{E^{吸收}}{E^{入射}} \end{align*}

单色吸收比：

\begin{align*} \alpha(\lambda,T) &= \frac{E_{\lambda}^{吸收}}{E_{\lambda}^{入射}} \\ r(\lambda,T) &= \frac{E_{\lambda}^{反射}}{E_{\lambda}^{入射}} \end{align*}

对不透明物体， $\alpha(\lambda,T)+r(\lambda,T)=1$
一个好的发射体一定也是好的吸收体
基尔霍夫定律（1860 年）：实验发现，在温度一定时物体在某波长 $\lambda$ 处的单色辐出度与单色吸收比的比值与物体及其物体表面的性质无关，即

\begin{align*} \frac{M_{1}(\lambda,T)}{\alpha_{1}(\lambda,T)} = \frac{M_{2}(\lambda,T)}{\alpha_{2}(\lambda,T)} = \cdots = M_{0}(\lambda,T) \end{align*}

黑体: 能完全吸收各种波长电磁波而无反射的物体。
- 吸收比和单色吸收比为 100%
- 黑体辐出度 $M_{0}$
- 在温度一定时黑体的单色辐出度与波长有关，并存在一极大值，所对应的极值点 $\lambda_{m}$ 有关系， $T\uparrow\to\lambda_{m}\downarrow$
- 斯特藩—玻耳兹曼定律： $M(T)=\sigma T^{4}$
- 维恩位移定律： $T\lambda_{m}=b$

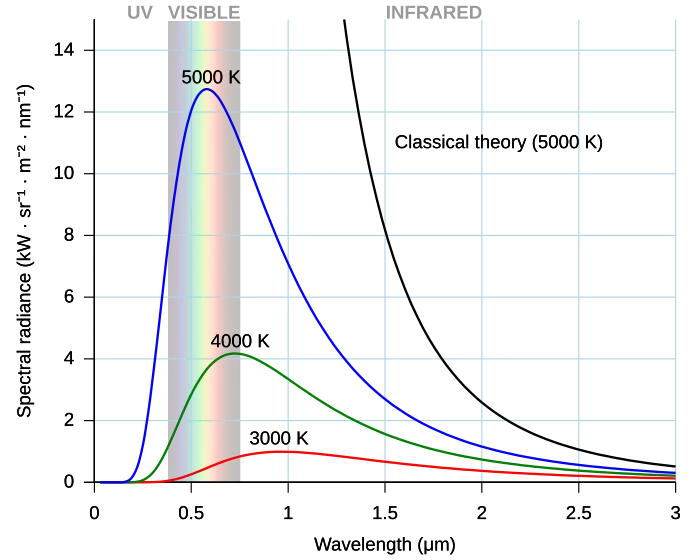
heiti

1.2 普朗克的能量子假说和黑体辐射公式#

普朗克黑体辐射公式：

\begin{align*} M_{0}(\nu,T) & = \frac{2\pi \nu^{2}}{c^{2}} \frac{h\nu}{e^{h\nu/kT}-1} \\ M_{0}(\lambda,T) & = \frac{2\pi hc^{2}\lambda^{-5}}{e^{hc/\lambda kT}-1} \end{align*}

普朗克常量：

\begin{align*} h=6.626\times 10^{-34}J\cdot s = 4.136\times 10^{-15}eV\cdot s \end{align*}

普朗克假定：对于频率为 $\nu$ $ν$ 的振子，振子能量不是连续的，而是分立的，它的取值是某一最小能量 $h\nu$ $h ν$ 的整数倍
- 能量子： $\epsilon=h\nu$

1.3 爱因斯坦的光量子假说#

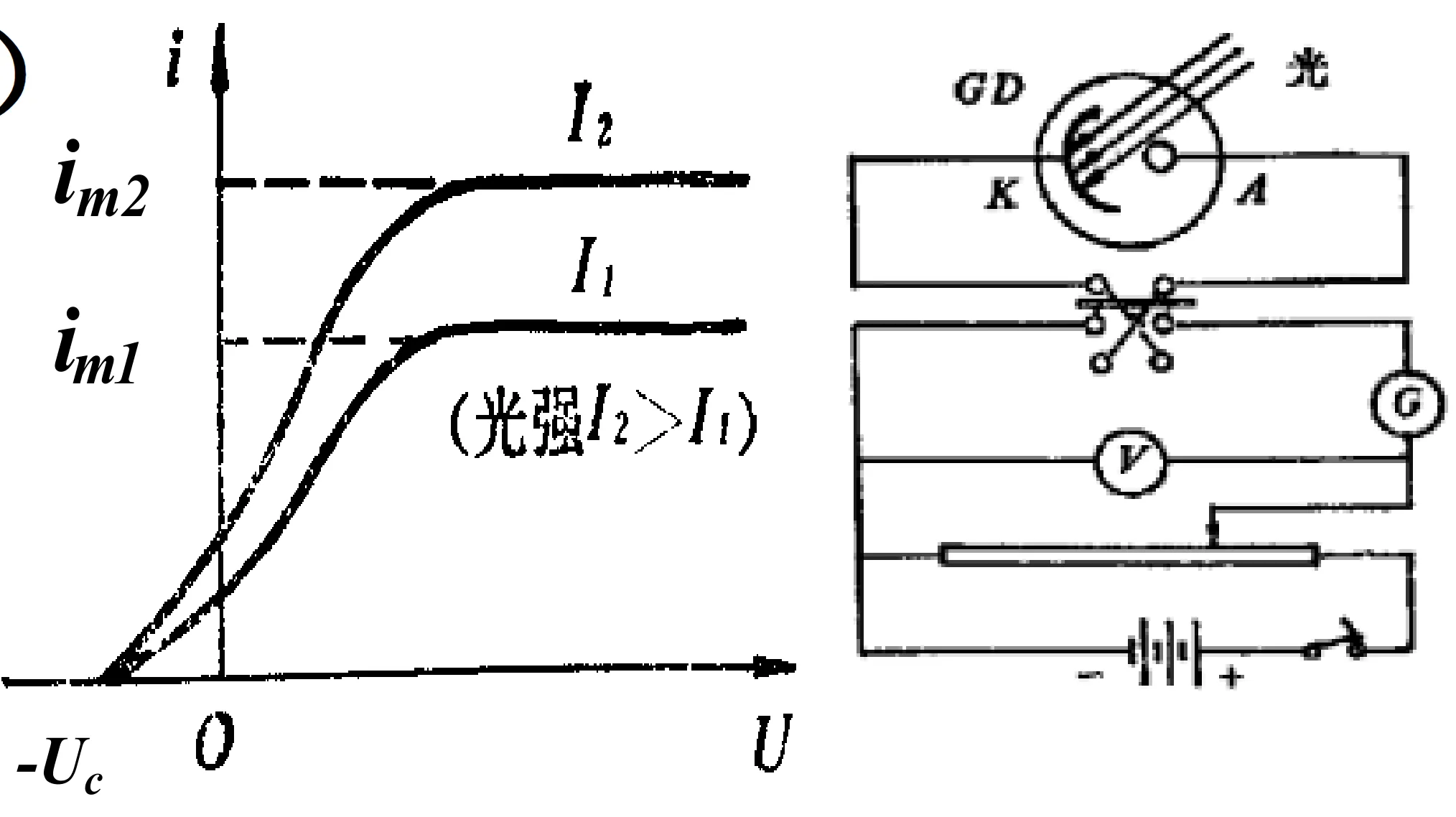
guangdianxiaoying

光电效应实验规律：
- 饱和光电流强度 $i_{m}$ $i_{m}$ 与入射光强 $I$ $I$ 成正比，还和单位时间光子数目成正比
  - 光强不变时，频率高，单个光子能量大，但单位时间光子数少
- $U_{c}$ $U_{c}$ ：遏止电压
  - $U_{c}=K\nu-U_{0}$ ， $K$ 与材料无关
  - 电子初动能： $E_{k}=\frac{1}{2}mv^{2}=eU_{c}$
  - 电子最大初动能： $eU_{c}=e(K\nu-U_{0})=Ke(\nu-\nu_{0})=h(\nu-\nu_{0})$ $e U_{c} = e (K ν - U_{0}) = Ke (ν - ν_{0}) = h (ν - ν_{0})$
    - $\nu_{0}$ ：截止频率或红限频率
- 光电效应是瞬时发生的
爱因斯坦光量子假设：电磁辐射由以光速 $c$ $c$ 运动的局限于空间某一小范围光量子（光子）组成，仍然保持频率的概念 $\epsilon=h\nu$ $ϵ = h ν$
- $\frac{1}{2}mv^{2}=h\nu-A$ ， $A$ ：逸出功，红限频率： $\nu_{0}=\frac{A}{h}$
光的波粒二象性：波动性特征 $\nu,\lambda$ $ν, λ$ ，粒子性特征 $E,m,p$ $E, m, p$
- 光作为电磁波是弥散在空间而连续的，光作为粒子在空间中是集中而分立的
- 光子在某处出现的概率由光在该处的强度决定，和该处光振幅的平方成正比

1.4 康普顿散射#

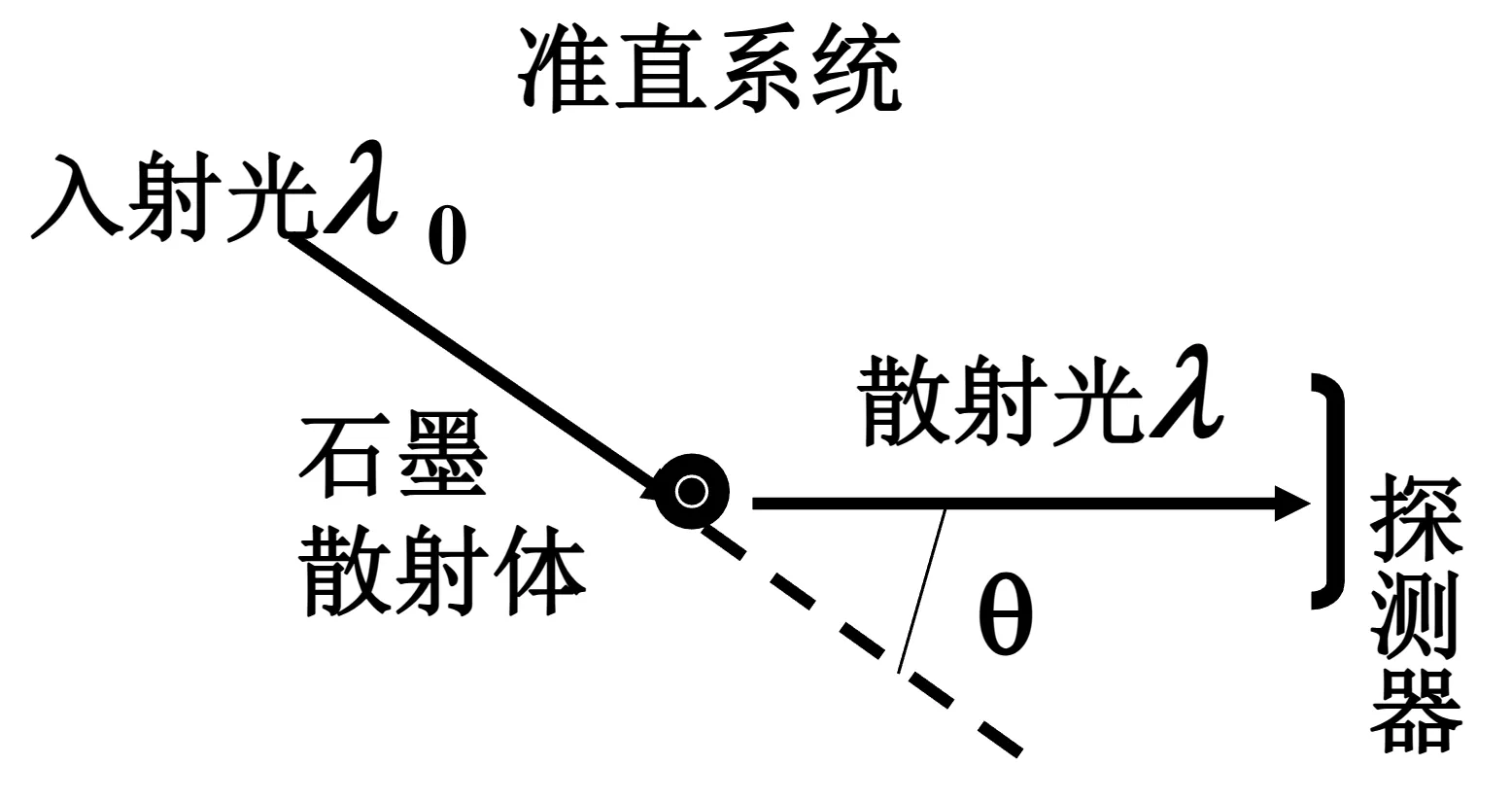
kangpudunsanshe

物质一定， $\theta$ 一定，研究 $I(\lambda)$

$\Delta\lambda=\lambda-\lambda_{0}$ ：除原波长 $\lambda_{0}$ 外，出现了移向长波方的新的散射波长 $\lambda>\lambda_{0}$
随原子序数的增大，原波长谱线强度升高而新波长的谱线强度降低

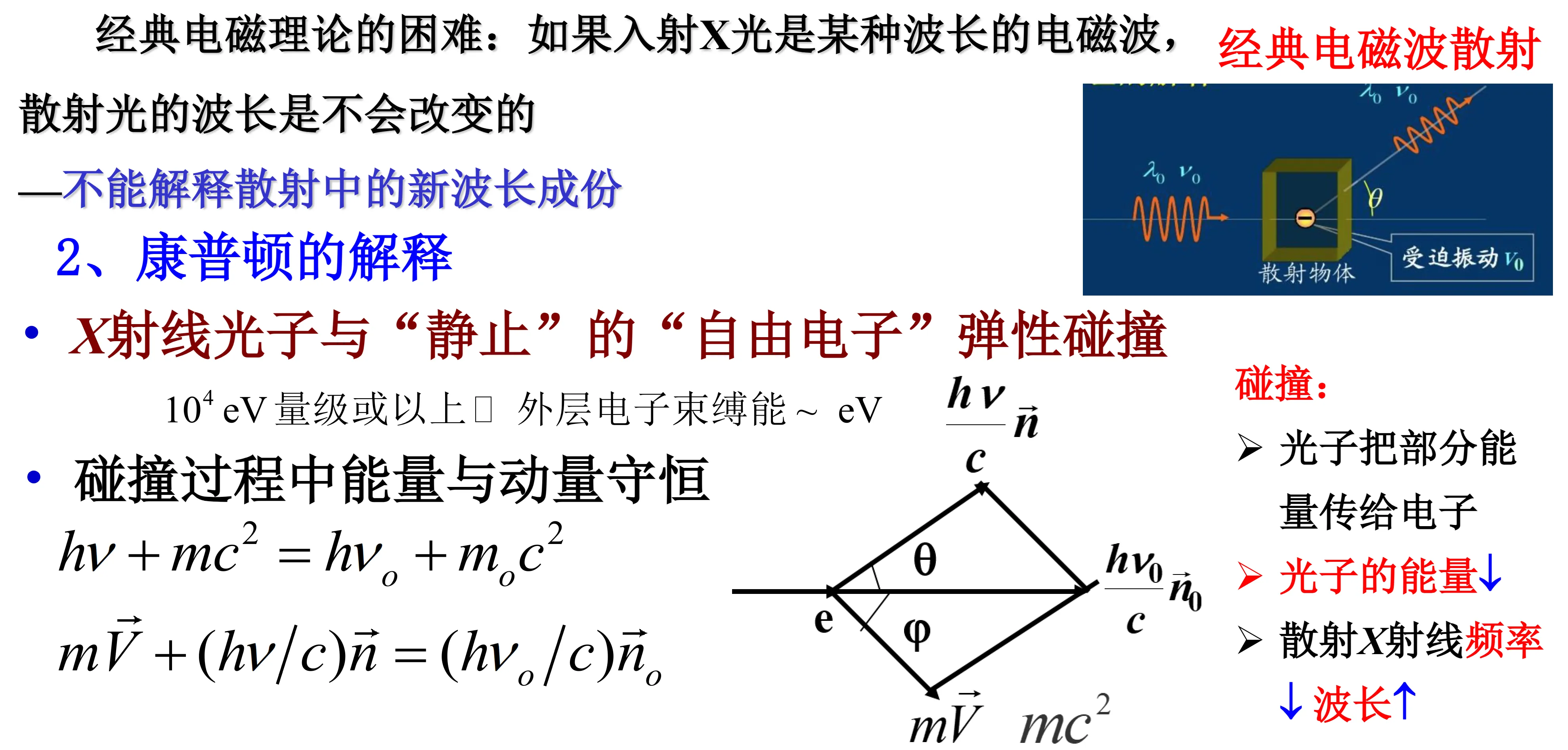
kangpudundejieshi

\begin{align*} \Delta \lambda=\lambda-\lambda_{0} = \frac{h}{m_{0}c}(1-\cos\theta)=\frac{2h}{m_{0}c}\sin^{2} \frac{\theta}{2} \end{align*}

对可见光来讲， $\frac{\Delta\lambda}{\lambda_{0}}\approx 10^{-5}$ 到 $10^{-6}$
证明了光量子具有动量的假设： $p=\frac{\epsilon}{c}=\frac{h\nu}{c}=\frac{h}{\lambda}$

1.5 氢原子光谱玻尔理论#

经典原子模型
- 汤姆逊父子的面包夹葡萄干模型
- 卢瑟福的 $\alpha$ 粒子散射实验和原子的核结构模型
波数：

\begin{align*} \tilde{\nu}=\frac{1}{\lambda} = R_{H}\left( \frac{1}{m^{2}}-\frac{1}{n^{2}} \right) = T_{m}-T_{n} \end{align*}

$T_{m},T_{n}$ $T_{m}, T_{n}$ ：光谱项
- $m$ 取不同值时，给出不同光谱系； $n$ 对应于不同谱线， $n>m$
$R_{H}$ ：里德伯恒量
玻尔假设：
- 定态条件： $E_{n}$ 能级
- 频率条件： $h\nu=E_{n}-E_{m}$
- 角动量量子化条件： $L_{n}=mv_{n}r_{n}=n \hbar$
氢原子半径：

\begin{align*} \frac{e^{2}}{4\pi \epsilon_{0}r^{2}} & = \frac{mv^{2}}{r} \\ L =mvr = n \hbar & = n \frac{h}{2\pi} \\ \implies r_{n} & = n^{2} \frac{\epsilon_{0}h^{2}}{\pi me^{2}} = n^{2}r_{1} \end{align*}

电子能量

\begin{align*} E & =\frac{1}{2}mv^{2} - \frac{e^{2}}{4\pi \epsilon_{0}r}= - \frac{e^{2}}{8\pi \epsilon_{0}r} \\ \implies E_{n} & = \frac{E_{1}}{n^{2}}, E_{1}=-13.6\mathrm{eV} \end{align*}

量子力学入门#

2.1 德布罗意假设#

物质波假设： $E=h\nu=\hbar\omega,\vec{p}=\frac{h}{\lambda}\vec{n}=\hbar k\vec{n}$
假设粒子沿 $x$ 轴正向运动，自由，能量 $E$ ，动量 $p$ ：

\begin{align*} \Psi(x,t)=Ae^{i(kx-\omega t)} = Ae^{\frac{i}{\hbar}(px-Et)} \end{align*}

宏观物体只表现出粒子性
电子绕核转动形成环形驻波： $2\pi r=n\lambda \implies L=mvr=n\hbar$
电子在无限深井中形成驻波

2.2 电子衍射实验#

布喇格方程： $n\lambda=2d\sin \phi$

balagefangcheng

2.3 波函数的统计解释#

波函数 $\Psi$ $Ψ$ 是描述粒子在空间概率分布的“概率振幅”，其模方 $\lvert \Psi(\vec{r},t) \rvert^{2}=\Psi(\vec{r},t)^{*}\Psi(\vec{r},t)$ $∣ Ψ (r, t) ∣^{2} = Ψ (r, t)^{*} Ψ (r, t)$ ，代表 $t$ $t$ 时刻，在坐标 $\vec{r}$ $r$ 附近单位体积中发现一个粒子的概率，称为“概率密度”
- 单值
- 有限：归一化条件
- 连续：一阶导数连续
双缝干涉中，干涉是概率波的干涉，由概率幅线性叠加产生

\begin{align*} \rho_{12}(\vec{r},t)=\lvert \Psi_{1}(\vec{r},t) + \Psi_{2}(\vec{r},t) \rvert^{2} \neq \lvert \Psi_{1}(\vec{r},t) \rvert ^{2} + \lvert \Psi_{2}(\vec{r},t) \rvert ^{2} \end{align*}

2.4 不确定度关系#

不确定度关系：粒子在同一方向上的坐标和动量不能同时确定

\begin{align*} \Delta x \cdot\Delta p_{x}\geq \frac{\hbar}{2} \end{align*}

buquedingxingguanxi

当 $\Delta x$ 越小， $\Delta v$ 就会越大，那么相应的 $v$ 就会越大
能量与时间的不确定度关系：
- $\Delta t$ ：粒子处于某量子态的寿命
- $\Delta E$ ：该量子态能量不确定范围

\begin{align*} \Delta E\cdot\Delta t \geq \frac{\hbar}{2} \end{align*}

2.5 薛定谔方程#

$x$ 方向上自由粒子薛定谔方程

\begin{align*} i\hbar \frac{ \partial }{ \partial t } \Psi(x,t)= - \frac{\hbar^{2}}{2m} \frac{ \partial ^{2} }{ \partial x^{2} } \Psi(x,t) \end{align*}

推广到势场中

\begin{align*} i\hbar \frac{ \partial }{ \partial t } \Psi(x,t)= \left[ -\frac{\hbar^{2}}{2m}\frac{ \partial ^{2} }{ \partial x^{2} }+U(x,t) \right] \Psi(x,t) \end{align*}

推广到三维情况

\begin{align*} i\hbar \frac{ \partial }{ \partial t } \Psi(\vec{r},t)= \left[ -\frac{\hbar^{2}}{2m}\nabla^{2}+U(\vec{r},t) \right] \Psi(\vec{r},t) \end{align*}

哈密顿算符

\begin{align*} \hat{H}=-\frac{\hbar^{2}}{2m}\nabla^{2} + U(\vec{r},t) \end{align*}

定态薛定谔方程
- $\Phi_{E}$ ：本证波函数
- $E$ 只有取一些特定值，解才能满足波函数的条件
- 判断波函数是否描述定态：计算 $\rho(\vec{r},t)$ 是否与 $t$ 有关，无关则为定态

\begin{align*} \Psi_{E}(\vec{r},t) &= \Phi_{E}(\vec{r})e^{- \frac{i}{\hbar}Et} \\ \implies \rho(\vec{r},t) &= \lvert \Phi_{E}(\vec{r}) \rvert ^{2} \end{align*}

记一系列定态解为

\begin{align*} \Psi_{n}(x,t)=\Phi_{n}(x)e^{- \frac{i}{\hbar}E_{n}t} \end{align*}

则通解可写为

\begin{align*} \Psi(x,t)=\sum_{n} C_{n}\Psi_{n}(x,t) = \sum_{n}C_{n}\Phi_{n}(x)e^{- \frac{i}{\hbar}E_{n}t} \end{align*}

可以证明

\begin{align*} C_{n}=\int _{-\infty}^{\infty} \Phi_{n}^{*}(x)\Psi(x,0) \, \mathrm{d}x \end{align*}

几率流密度矢量

\begin{align*} i\hbar \frac{ \partial }{ \partial t } \Psi & = \left[ -\frac{\hbar^{2}}{2m}\nabla^{2}+U \right]\Psi \\ -i\hbar \frac{ \partial }{ \partial t } \Psi^{*} & = \left[ -\frac{\hbar^{2}}{2m}\nabla^{2} + U \right]\Psi^{*} \\ \implies i\hbar \frac{ \partial }{ \partial t } (\Psi^{*}\Psi) & = \frac{\hbar^{2}}{2m}\nabla \cdot(\Psi \nabla \Psi^{*}- \Psi^{*}\nabla \Psi) \end{align*}

记几率流密度矢量为：

\begin{align*} \vec{J} = \frac{i\hbar}{2m}[\Psi \nabla \Psi^{*} - \Psi^{*}\nabla \Psi] \end{align*}

则

\begin{align*} \frac{ \partial }{ \partial t } \rho + \nabla \cdot \vec{J} = 0 \end{align*}

积分形式：

\begin{align} \frac{\mathrm{d}}{\mathrm{d}t}\int_{\tau}\rho(\vec{r},t)\mathrm{d}\tau = -\int_{\tau}\nabla \cdot \vec{J}\mathrm{d}\tau = - \int_{S}\vec{J}\cdot \mathrm{d}\vec{S} \end{align}

其中 $S$ 为体积 $\tau$ 的表面

几率密度： $\rho=\Psi^{*}\Psi$ $ρ = Ψ^{*} Ψ$
- $eN\rho$ ：电荷密度
- $eN\vec{J}$ ：电流密度矢量

2.6 态叠加原理#

若 $\Psi_{1},\Psi_{2},\dots,\Psi_{n}$ $Ψ_{1}, Ψ_{2}, \dots, Ψ_{n}$ 是体系的一些列可能的状态，则其线性叠加也是体系的一个可能的状态， $\Psi=C_{1}\Psi_{1}+C_{2}\Psi_{2}+\dots +C_{n}\Psi_{n}$ $Ψ = C_{1} Ψ_{1} + C_{2} Ψ_{2} + \dots + C_{n} Ψ_{n}$
- 若 $\{ \Psi_{i} \}$ 正交归一，那么当体系处于 $\Psi$ 态时，发现体系处于 $\Psi_{k}$ 态的概率为 $\lvert C_{k} \rvert^{2}$

量子力学深入 ---- 量子力学中的力学量#

3.1 动量的算符表示#

具有确定动量的运动状态：

\begin{align*} \Psi_{\vec{p}} = A\exp\left( \frac{i}{\hbar}\vec{p}\cdot \vec{r} \right) \end{align*}

晶体衍射后，动量连续

\begin{align*} \Psi(\vec{r},t)=\int C(\vec{p},t)\exp\left( \frac{i}{\hbar}\vec{p}\cdot \vec{r} \right) \frac{\mathrm{d}\vec{p}}{(2\pi \hbar)^{3/2}} \end{align*}

这里 $\mathrm{d}\vec{p} = \mathrm{d}p_{x}\mathrm{d}p_{y}\mathrm{d}p_{z}$ ，动量测量值在 $p$ 到 $p+\mathrm{d}p$ 区间的几率为 $\lvert C(p,t) \rvert^{2}\mathrm{d}p$

$x$ 平均值：

\begin{align*} \bar{x}=\int_{-\infty}^{\infty}\Psi^{*}(x,t)x\Psi(x,t)\mathrm{d}x \end{align*}

势能平均值

\begin{align} \bar{V} = \int_{-\infty}^{\infty} \Psi^{*}(x,t)V(x)\Psi(x,t)\mathrm{d}x \end{align}

但对于动量平均值，不能用 $\Psi(x,t)$ ，因为它是位置表象的；而应该用动量表象的 $C(p,t)$ ：

\begin{align*} \bar{p} = \int_{-\infty}^{\infty}C^{*}(p,t)pC(p,t)\mathrm{d}p \end{align*}

当然，也可以推导得到：

\begin{align*} \bar{p}=\int_{-\infty}^{\infty}\Psi^{*}(x,t)\left( -i\hbar \frac{ \partial }{ \partial x } \right) \Psi(x,t)\mathrm{d}x \end{align*}

在三维中，另外两维同理。

对于其他任意力学量，都可以表示为坐标和动量的形式，从而像上面那样计算平均值

\begin{align*} A(\vec{r},\vec{p}) \to \hat{A}(\vec{r},-i\hbar \nabla) \end{align*}

如动能为（联系薛定谔方程）

\begin{align*} \frac{p^{2}}{2m} \to -\frac{\hbar^{2}}{2m}\nabla^{2} \end{align*}

量子力学基本假设：每一个力学量 $A$ （不限于经典的力学量，如自旋）都与一个算符 $\hat{A}$ 相对应

\begin{align*} \bar{A}=\iiint \psi^{*}\hat{A}\psi \mathrm{d}x\mathrm{d}y\mathrm{d}z \end{align*}

3.2 算符的性质#

算符是指作用在一个函数上得出另一个函数的运算符号。态叠加原理要求量子力学中的力学量算符是线性算符，还要是厄密算符：满足对任意两个波函数 $\psi$ 和 $\phi$ ，有

\begin{align*} \int \psi^{*}\hat{F}\phi \mathrm{d}\tau=\int(\hat{F}\psi)^{*}\phi \mathrm{d}\tau \end{align*}

厄密算符的本征值为实数
在任何状态下，厄密算符的平均值为实数
厄米算符的分立谱所有本征函数都是正交归一化的

本征值：算符作用于函数有 $\hat{F}u=\lambda u$ ，则 $\lambda$ 为 $\hat{F}$ 的本征值， $u$ 为 $\hat{F}$ 的本证函数

动量算符的本证函数： $\Psi_{p}(x)=Ce^{ipx/\hbar}$

狄拉克符号：

\begin{align*} \bar{F}= \langle\hat{F}\rangle = \bra{u} \hat{F}\ket{u} = \int u^{*}\hat{F}u\mathrm{d}x \end{align*}

若 $\psi(x)$ 已归一化，则

\begin{align*} &\langle \psi, \psi \rangle = \sum_{k,l} c_{k}^{*}c_{l}\int u_{k}^{*}u_{l}\mathrm{d}x = \sum_{k,l}c_{k}^{*}c_{l}\delta_{kl} = \sum_{l}\lvert c_{l} \rvert ^{2}=1 \\ &\langle\hat{F}\rangle=\sum_{l}\lvert c_{l} \rvert ^{2}\lambda_{l} \end{align*}

验证厄米算符：定义/上面的性质

一般情况下，算符之积不满足交换律，记 $[\hat{A},\hat{B}]=\hat{A}\hat{B}-\hat{B}\hat{A}$ ，有 $[\hat{x},\hat{p}_{x}]=i\hbar$

3.3 动量算符和角动量算符#

角动量算符：

\begin{align*} \hat{L}=\hat{r}\times \hat{p} = -i\hbar(\vec{r}\times \nabla) \end{align*}

满足

\begin{align*} &[\hat{L}_{x},\hat{L}_{y}] = i\hbar \hat{L}_{z} \\ &\hat{L}\times \hat{L} = i\hbar \hat{L} \\ \end{align*}

qiuzuobiaoxizhongdejiaodongliang