Kinnari's Blog

第一段科研的总结和宣传

20 min

距离这篇工作结束已经过去一周多一些了，实际上是拖延症晚期拖到现在决定写一篇文章来记录一下这段科研。实际上这应该不算第一段，在此之前也进组打过工，但是由于种种原因并没有什么产出，更不用提以第一作者的身份发表文章，故而这些均不被我算作是第一段科研。我大概想从 idea、写作等方面来简单写写我的一些认知，其中不免有幼稚甚至错误的部分，还望能在评论中指出。

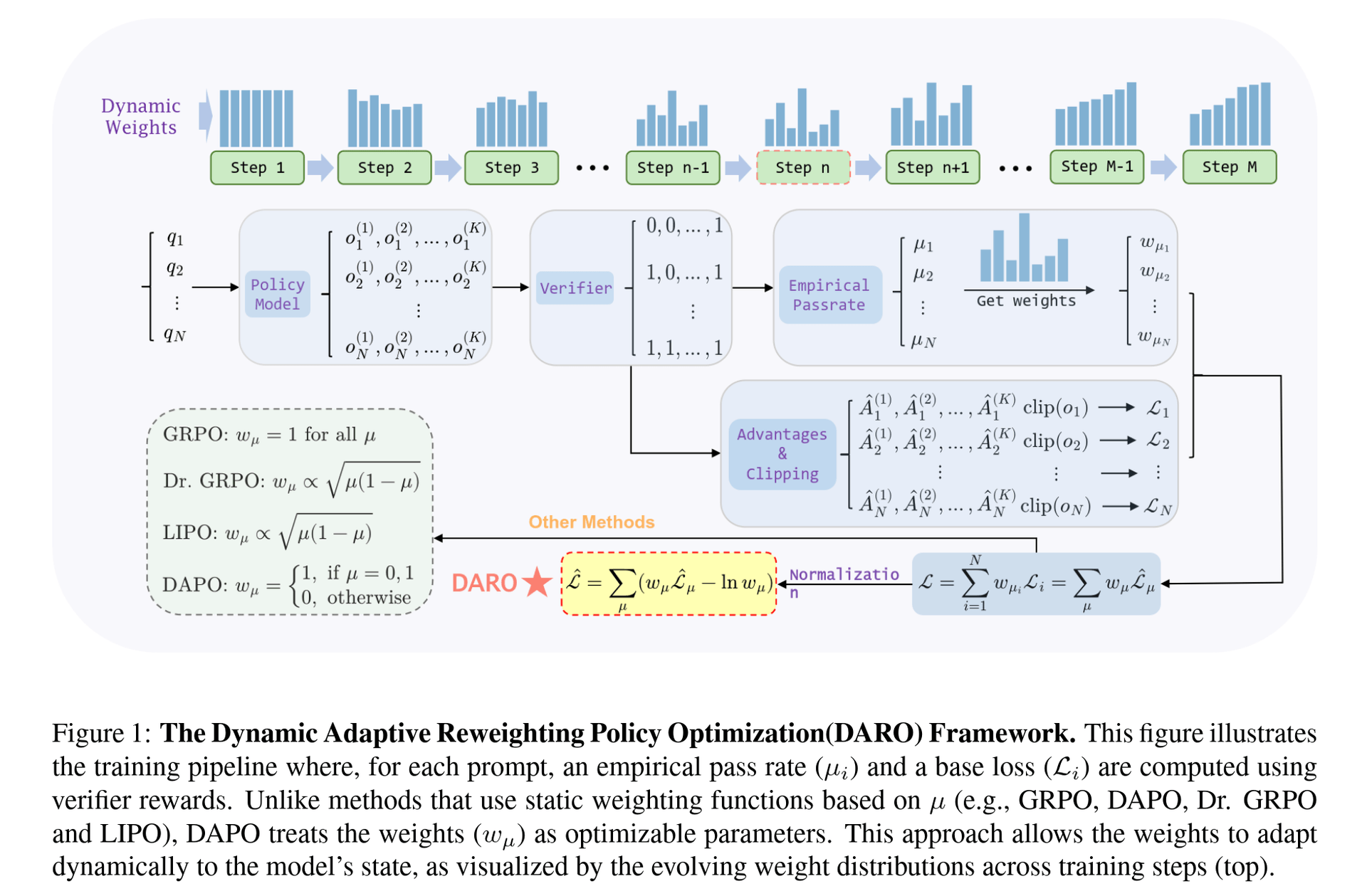
基本情况

因为我本人一直对于 RL + LLM 这一块，准确来说是 RLVR，十分感兴趣，才不是因为这一块的数学公式比起其他同为灌水的方向更多，所以在最初选题的时候就选择了这一方向。在我开始调研这一方向的时候（五月底六月初），其实已经发现 RL 文本推理其实已经卷麻了，一些过于简单的 idea 已经不足以抢着就能发论文，因此在整个工作期间我和带我的学长都处于一种焦虑的状态，担心我们的 idea 随时会被其他组抢发。

不得不提到的是，在开始这段经历前我曾拜读过大名鼎鼎的 DAPO 这篇文章，被其中几个优雅且一看就有效的 trick 给迷上了，因此也萌发了超越 DAPO 的念头（这也是之后选用 DAPO 作为 baseline 之一的原因）。在最后的分析和提出统一损失框架的时候，也是 DAPO 给了我最初的灵感。

此外，这次合作的学长 TheRoadQAQ 也是 nice 中的 nice，不仅本人做过文本的 RLVR，对这个方向了如指掌，而且在整个过程中，从最初 idea 的讨论，数据集的选择到最后的写作，都狠狠地 carry 了我一把，可以说没有他就没有这篇工作的最终完成，在这里感谢一波学长的大力帮助🙏。

Idea

最初我们希望能够通过课程学习的办法来加快 RL 训练的收敛速度，最终目标是缩短训练所需的时间，涉及到难度估计与更少的 rollout 次数。最开始我和学长的想法是通过在同一 batch 中以难度为依据重复采样的方式来进行更高效率的学习。当时一些工作，例如上面提到的 DAPO 以及 https://arxiv.org/pdf/2504.03380 等等文章，认为给模型训练中等难度的题目提升更大，因此我们使用了一个均值为 0.5（难度区间为 [0,1][0,1]），标准差为 0.1 的高斯分布进行采样，均值保证了中等难度的题目被采样到的概率最大，方差则由 3σ3\sigma 准则保证了采到的样本难度集中在 [0.2,0.8][0.2, 0.8] 之间，正好剔除了难度过高和过低的样本，并且随着训练的进行，中等难度的题目集合也会发生变化，从而自动实现了课程学习的初衷。

初步的实验结果表明这样的采样策略是有效的，但是在更换数据集或模型后的表现却和 DAPO 差不多，有的甚至低于原始的 GRPO，并且在训练后期，因为模型能力大大提升，数据集中的样本多为完全没法做出和完全正确的两类，导致对一些难度适中的样本重复采样次数过多，训练极其容易崩溃。为了分析这种崩溃，我从样本优势（advantage，下面简称 adv）的角度进行了思考，发现所谓重复采样不过是给优势乘上了一个系数（后续称为权重）。GRPO 中原始的 adv 为：

A=r−μσA=\frac{r-\mu}{\sigma}

而对于一个被重复采样了 nn 次的样本来说，它的 adv 为：

A^=r−μ^σ^, where μ^=μ,σ^=σn\hat{A}=\frac{r-\hat{\mu}}{\hat{\sigma}}, \text{ where } \hat{\mu}=\mu, \hat{\sigma} = \frac{\sigma}{\sqrt{n}}

也就是说 A^=nA\hat{A}=\sqrt{n}A。这意味着最终的 adv 为原始 adv 的离散加权形式，权重分别为 1,2,…,n,…\sqrt{1}, \sqrt{2}, \dots, \sqrt{n}, \dots。而这样人为约定+随机获得的加权权重，显然不太可能碰巧就是最优加权形式，因此，我们将目光转向了如何设计一个最优的权重来提高每个样本的利用率，从而加速收敛。

又显然的，最优权重会受到多个因素的影响，包括模型能力、数据集、训练阶段等等，因此几乎不可能被人为设计出来。故我们认为这样的最优权重一定只能是模型自己学到的，而不能交给人类来做，所以这时我们的 idea 就变为了为每一个样本配置一个可学习的权重，在训练的反向传播时同步更新这一个权重，从而尝试获得最优权重。事实上，类似的想法在其他的一些论文中也有出现，例如用经典的 UCB 等方法来学习一个合适的权重。我们认为这些方法也有人为设计的成分，这是我们不希望的，我们希望这些权重能够完完全全由模型自己来学习。

想法虽然很美好，但是在实际的训练中难免会遇到一些问题。最严重的问题当属在一次完整的训练中，每一个样本被训练的次数可能不会超过个位数，例如训练 500 步，每一步的 batch size 为 128，数据集样本个数为 45k 的情况下，平均每个样本只会被利用 500∗128/(45∗1024)=1.39500 * 128 / (45 * 1024) = 1.39 次，最差的情况下一个样本仅仅只会被模型“见到”一次，为它单独学习一个最优权重基本上可以说是天方夜谭。另一方面，从理论上来讲，仅仅是为每一个样本设置一个权重还不够，模型可能会学习到一些“窍门”来降低损失（称为权重 hack），例如如果 loss 都大于 0 的话，模型只需要学习每个权重为 -inf 即可让损失降到最低。因此，我们的思路又被打断了。

既然为每一个样本单独设置一个权重是不现实的，那么有没有一种妥协的办法，能够利用样本自带的某些性质，给样本分类后，给更大的类这个级别来加权呢？这时候我们将目光投向了 DAPO。在 DAPO 中，难度为 0 或者 1 的样本被完全剔除了，在他们的具体代码实现中，体现为筛除平均奖励（也就是样本在 rollout 中的通过率，下面都以通过率统称）为 0 或 1 的样本。这提醒我们，对每个 batch，在 rollout 结束并计算出奖励后，就可以根据通过率来为样本分组了！如果总共有 KK 次 rollout，那么就可以分类为通过率 {0,1/K,2/K,…,K/K}\{0, 1/K, 2/K, \dots, K/K\} 共 K+1K+1 类，也就只需要引入一个形状为 (K+1,) 的张量即可实现加权的效果。这样带来了若干好处：

  1. 几乎在每一步，所有通过率的样本都会出现，从而对应的权重也能得到持续的更新，这巧妙地避免了上面我们提到的最大的问题。
  2. 实现这个加权只需要引入一个长度为 K+1K+1 的张量，与数据无关，与模型无关，几乎不会带来额外的计算开销和存储开销。
  3. 通过模型自主学习权重，能够隐式地实现课程学习，提高训练效率。

这时候只剩下最后一个问题了，即上面提到的“权重 hack” 的问题。这个问题比较好解决，只需要添加一个惩罚项即可。记通过率 μ\mu 对应的损失为 Lμ\mathcal{L}_\mu，权重为 wμw_\mu，惩罚项为 N(wμ)N(w_\mu)，那么最终的损失形式为：

L^=∑μ(wμLμ+N(wμ))\begin{equation} \hat{\mathcal{L}} = \sum_{\mu} \big(w_\mu \mathcal{L}_\mu + N(w_\mu)\big) \end{equation}

该如何得到这个惩罚项 N(⋅)N(\cdot) 呢？我们希望这个项能够足够的合理，而不是简单粗暴地尝试几个常用的项后选择最好的一个使用。注意到这个项也会影响到最终的收敛状态，因此我们决定回到起点，从 GRPO 的损失开始进行分析，即分析 Lμ\mathcal{L}_\mu 的性质。我们可以推导得到，在使用了 token-mean 作为聚合损失的方式的情况下（使用这种方式是因为在 Lite PPO 中的实验表明这种方式的效果更佳），GRPO 的损失可以表示为

LGRPO=Eq∼Q,{oi}i=1K∼πθold(⋅∣q)[∑i=1K∣oi∣Lf(Ai,oi)],f(A,o)={min⁡{r(θ)A,(1+ϵ)A},A>0max⁡{r(θ)A,(1−ϵ)A},A<0\begin{equation} \begin{split} &\mathcal{L}_{GRPO} = \mathbf{E}_{q\sim \mathcal{Q},\{ o_{i} \}_{i=1}^{K}\sim \pi_{\theta_{old}}(\cdot|q)} \left[\sum_{i=1}^{K} \frac{\lvert o_{i} \rvert}{L} f(A_i, o_{i})\right], \\ &f(A,o) = \begin{cases} \min \{ r(\theta )A,(1+\epsilon)A \}, & A>0 \\ \max_{}\{ r(\theta)A, (1-\epsilon)A \}, & A<0 \end{cases} \end{split} \end{equation}

其中 Q\mathcal{Q} 为数据集，θ\theta 为模型参数，LL 为回复长度之和，f(⋅)f(\cdot) 为抽象出的 adv-clip 过程。具体推导细节见我们的论文 https://arxiv.org/abs/2510.09001。在此基础上，结合霍夫丁不等式，我们可以推导得到在训练的一步中 Lμ\mathcal{L}_\mu 可以用下面的式子进行近似：

Lμ≈∑o is pos∣o∣−∑o is neg∣o∣Lμ(1−μ)\begin{equation} \begin{split} \mathcal{L}_\mu\approx \frac{\sum_{o\text{ is pos}} \lvert o\rvert - \sum_{o\text{ is neg}} \lvert o\rvert}{L} \sqrt{\mu(1-\mu)} \end{split} \end{equation}

我们的实验结果表明这是一个非常优秀的近似，可以见论文中的 Figure 2，如下：

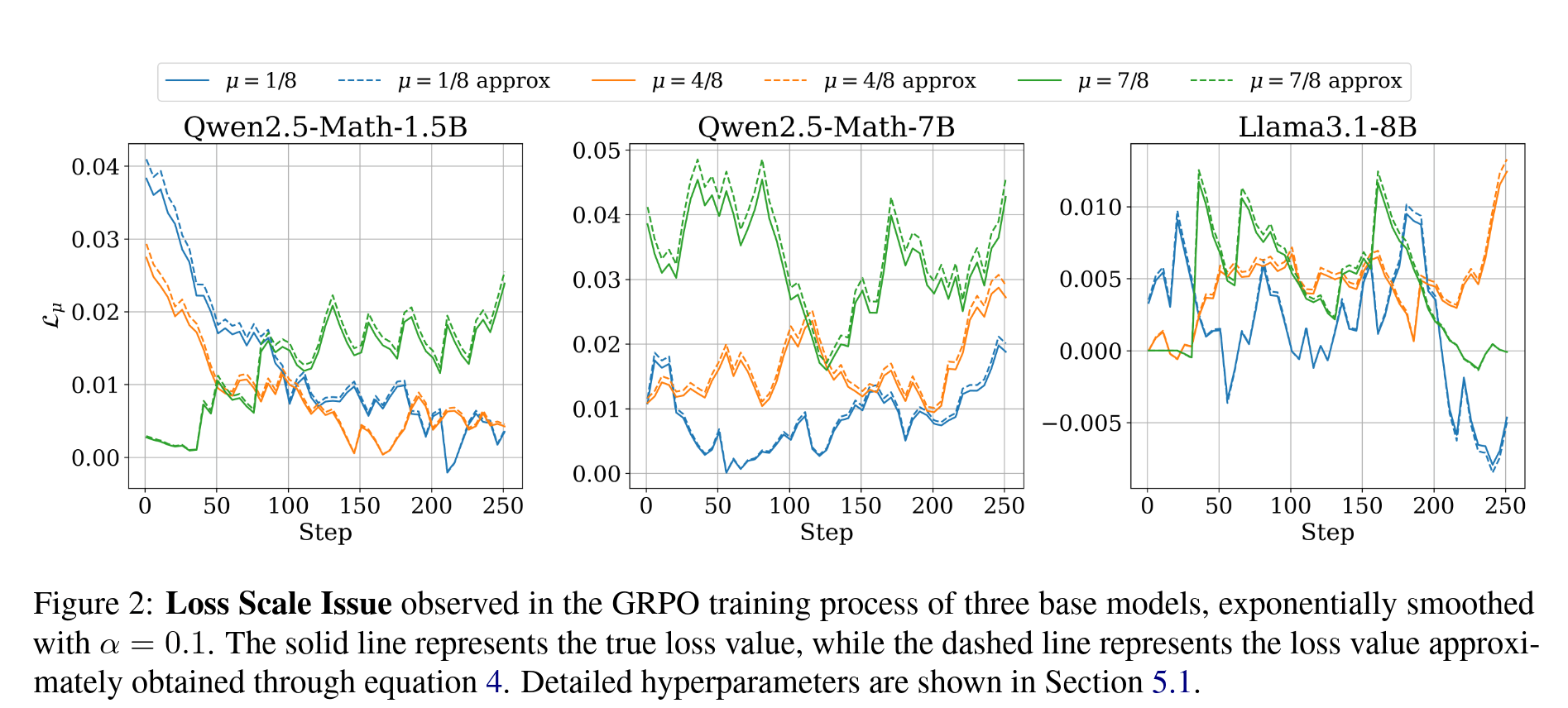
从这个图中我们还不难发现一个事实，那就是 Lμ\mathcal{L}_\mu 的大小是和模型、训练进度，以及最重要的 μ\mu 相关的。从近似值中可以看出，这一结果也成立，因为涉及到了 μ(1−μ)\sqrt{\mu(1-\mu)} 以及回复长度这两个值，而后者在几个工作中（如 Lite PPO）都有提到和 μ\mu 紧密相关，我们也做了相应的实验来验证这个结论，如论文中的 Figure 3 以及附录中的 Figure 6。

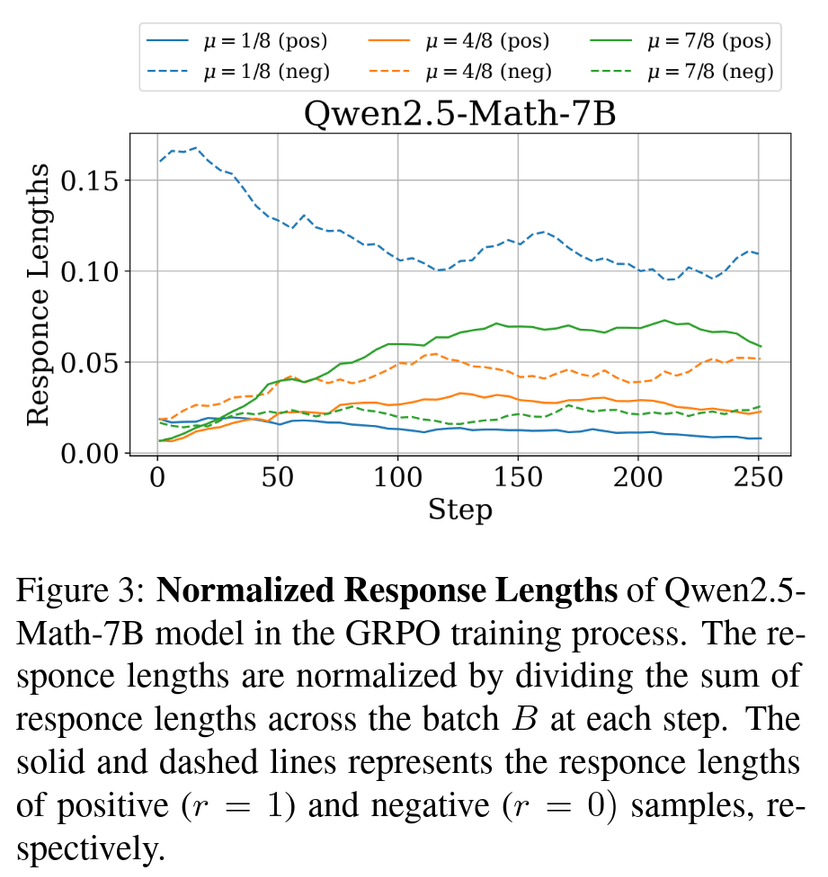
那么很显然，在 GRPO 算法中，loss 值的大小会随 μ\mu 而发生变化。对 Figure 2 的进一步观察可以得到，始终会有某些或某个 μ\mu 对应的 Lμ\mathcal{L}_\mu 会占据主导地位。这会导致模型过多的聚焦于某一种难度的样本，这显然是不妙的，很有可能会造成训练效率上的降低。于是如何设置惩罚项便明了了：我们需要这个惩罚项在收敛时能够让模型均匀的聚焦于每一种难度的样本上，体现在公式中即为 wμLμ=Cw_\mu\mathcal{L}_\mu= C，和 μ\mu 无关。为了保持权重学习的自由，我们将这一目标作为最终的收敛条件，从而就能解出想要的惩罚项 N()˙N(\dot)。对损失 L^\hat{\mathcal{L}} 求 wμw_\mu 的偏导，得到：

∇wμL^=Lμ+N′(wμ)=0.\nabla_{w_{\mu}}\hat{\mathcal{L}}=\mathcal{L}_{\mu} + N'(w_{\mu}) = 0.

代入 wμLμ=cw_\mu\mathcal{L}_\mu= c 可以解得 Lμ=Cwμ−1\mathcal{L}_\mu = Cw_\mu^{-1}。又联想到 DAPO 中数据过滤的操作，将 μ=0,1\mu=0,1 的样本筛除掉，那么就得到了损失的最终形式：

L=∑μ≠0,1(wμLμ−ln⁡wμ),\begin{equation} \mathcal{L} = \sum_{\mu\ne0,1} (w_{\mu}\mathcal{L}_{\mu}-\ln w_{\mu}), \end{equation}

至此，整个 idea 基本完成，具体算法见 Algorithm 1。还剩下我们关于若干个 RLVR 算法的统一框架的提出，这部分内容我只放结论在这里，具体推导细节见我们的论文 https://arxiv.org/abs/2510.09001。我们可以将 GRPO、DAPO、Lite PPO 以及 Dr.GRPO 统一为如下形式：

LBASE=Eq∼Q,{oi}i=1K∼πθold(⋅∣q)[∑i=1Kwi⋅∣oi∣Lf(Ai,oi)].\begin{equation} \begin{split} \mathcal{L}_{BASE}=& \mathbf{E}_{q\sim \mathcal{Q},\{ o_{i} \}_{i=1}^{K}\sim \pi_{\theta_{old}}(\cdot|q)} \left[\sum_{i=1}^{K} w_i\cdot \frac{\lvert o_{i} \rvert}{L} f(A_i, o_{i})\right]. \end{split} \end{equation}

其中权重 wiw_i 的表达式如下：

AlgorithmWeight
GRPOwi=1w_i = 1
DAPOwi=I(0<μ<1)w_i=\mathbb{I}(0<\mu<1)
Lite PPOwi∝μ(1−μ)w_{i} \propto \sqrt{\mu(1-\mu)}
Dr.GRPOwi∝μ(1−μ)w_i \propto \sqrt{\mu(1-\mu)}

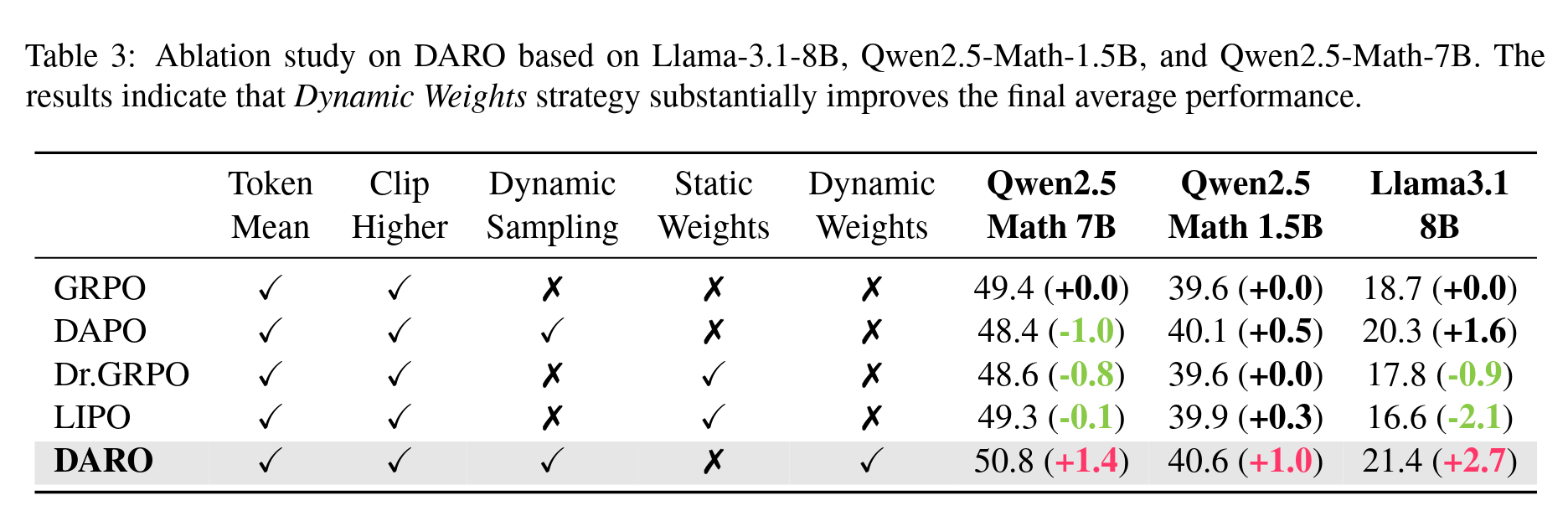
由此可见，这几个方法本质上都是对 GRPO 的简单加权方式，并不具备成为最佳加权方式的可能性，我们的 DARO 方法的优越性最体现在这里。更详细的分析也请见论文。这里再放一些结果图

一些结果图表

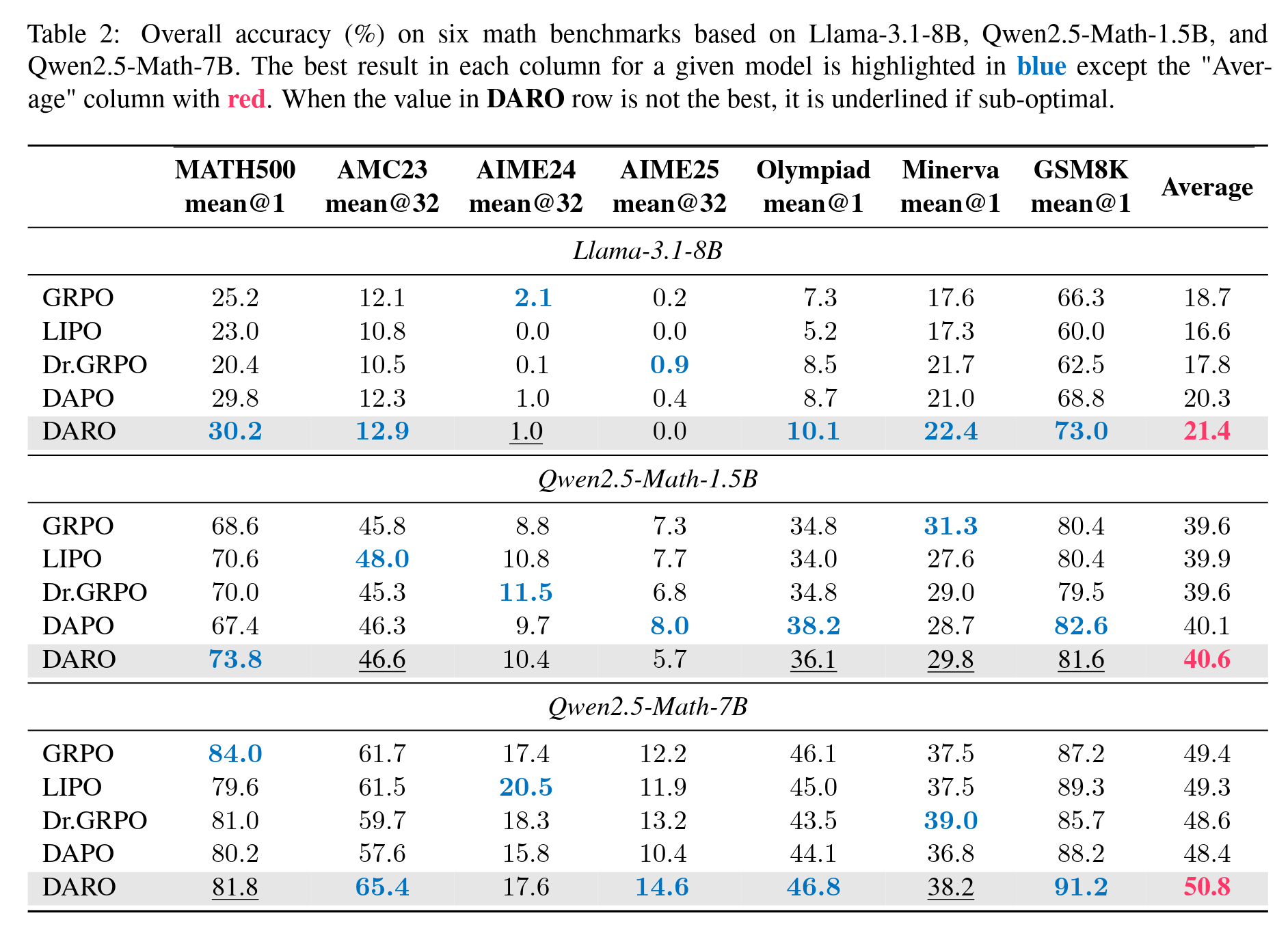
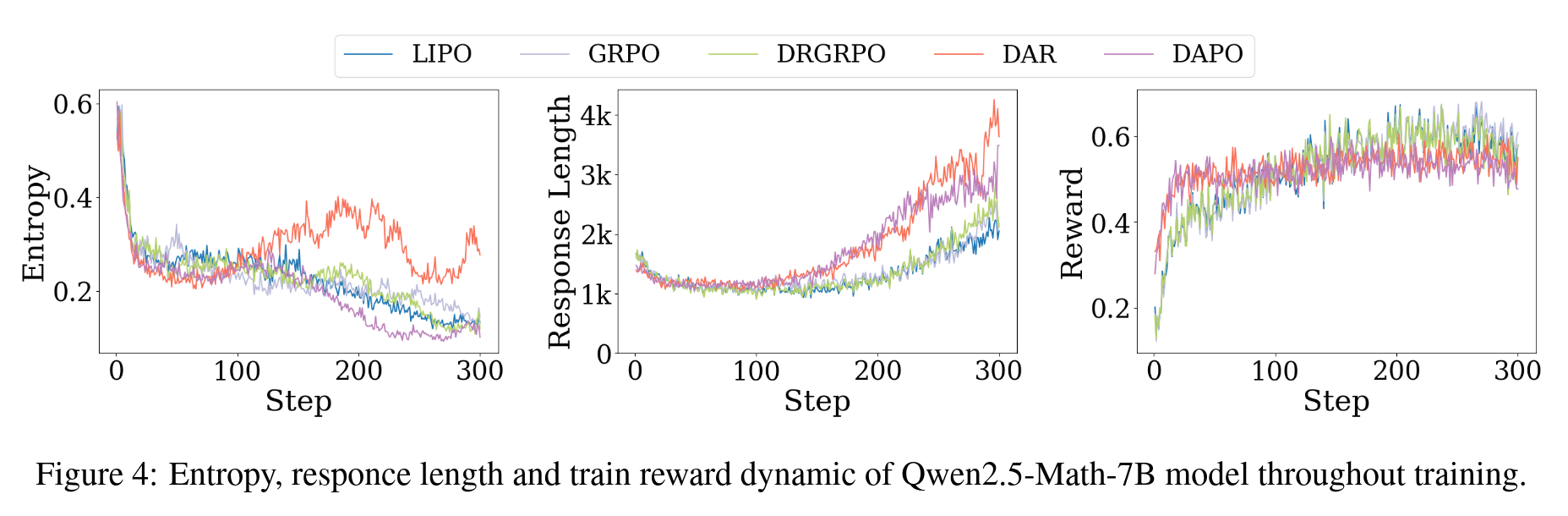
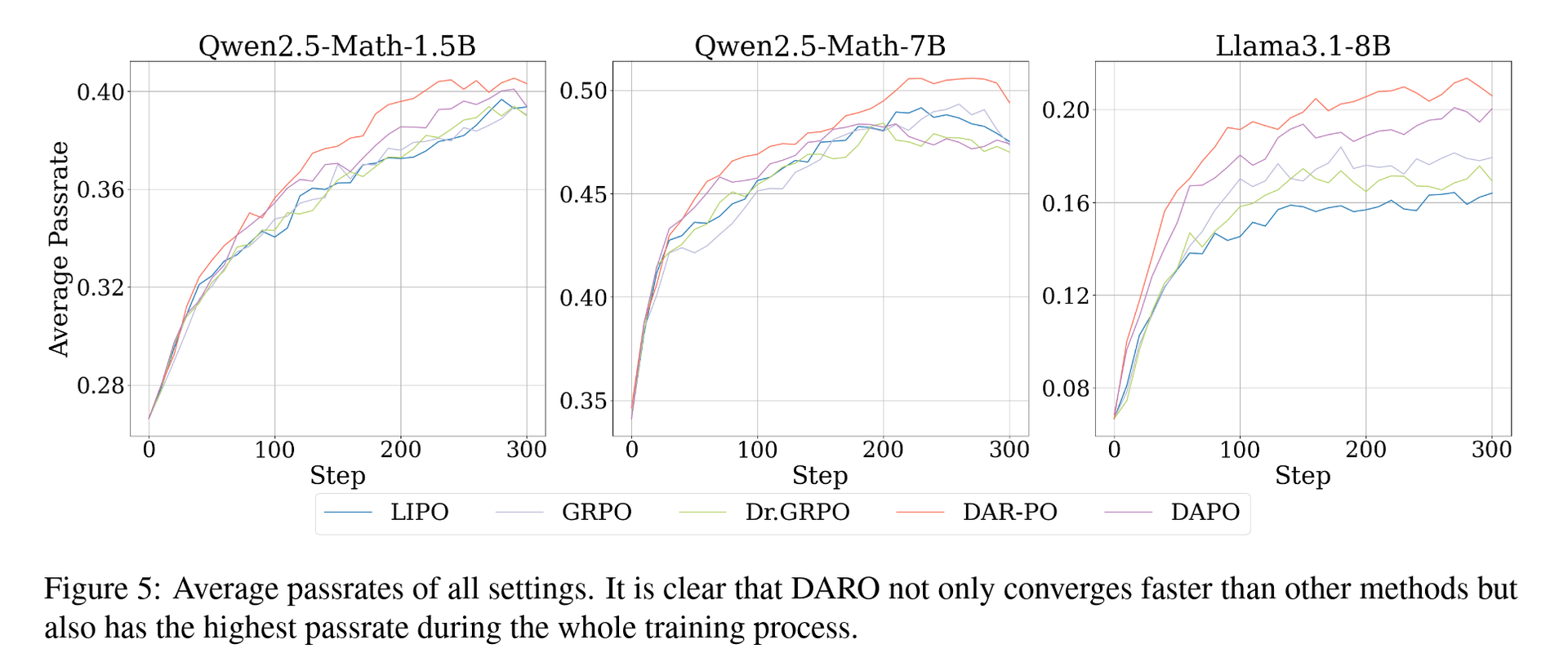
写作

事实证明，我本人的英文写作能力有点过于烂了，常见的论文用语都记不住多少，让我直接用英文开写实在是有点吃力。因此我选择了相对轻松一点的写法，先用中文写一遍大致内容，然后再翻译成英文进行修改，最后英文版写完后再用 ai 进行润色。需要注意的点是在润色时可以同时让 ai 告诉自己每一处改的依据，这样既可以学到更“学术”的表达，也可以检查 ai 的修改是否正确。

这里我推荐看 GAMES003 里面关于写作的讲解，还是比较不错的，就我自己而言，总结出来的要点主要有

  1. 写作需要有所谓 “flow” 的感觉，即一段话需要一个中心观点，这段话只需要讲好这个观点就行，不要一段话写太多东西；然后不同段的观点可以连缀成一个连贯的故事。
  2. 不要以一个做实验的人的角度写，而是站在读这篇论文的人的角度向他展示这篇文章做了什么，他能不能最舒适地明白这篇论文在干什么（即需要非常轻松的达到入脑的效果）。目前我还达不到这个境界😢
  3. 整篇文章的表格、图片的风格需要一致，最好是提前准备好一套令人舒适的调色方案
  4. pipeline 类的图用 PPT 画，实操还是很容易上手的；其他图用 matplotlib
  5. 每一段文字的最后最好不要刚好多出一点点，这样会不美观
  6. 只写一遍是肯定不行的，至少要拿出一周的时间反复修改

写作这一块我实在是太菜了，全靠学长的大力 carry 才能让论文出来，感动😭。

其他

在论文之外，我还有一些不太完整的想法，简单记录在下面。

关于方向的选择：我个人觉得当前的大模型领域实在是太卷了，如果一个方向入场太晚难免会面临很多困难，比方说

  1. 文本推理里面的各种算法被提出得太多，low-hanging fruit 被摘得太多，要提出新的且有用的东西的难度难免上升
  2. 入场太晚，在论文接收时也会遭遇和当时的热门小领域的区别对待，大家看多了都会厌倦，要是入场太晚难免会受到这种 debuff，比方说今年 NeuIPS 里面对投机解码的录取率就非常堪忧
  3. 入场太晚，基本上大家都在刷榜，你的方法即使有用且新颖，分数上打不过别的算法的话，也会天然被人低看一等

当然入场太早也会有很多弊端和优点，这里不一一列举了。我没什么较好的权衡策略，毕竟我也还是在其中沉浮的一个分母，看不清整个局势。

关于实验：最开始一定要调参！多调参，找到在所有模型和数据集上都合适的一组参数，然后再进行全量实验。虽然调参也会花费时间，但是能极大的避免一组参数在一个模型上正常训练，但另一个模型上崩溃的情况。

关于投稿量：今年开始各大会议的投稿量激增，其中很大的一个原因就是太多人入场，提交甚至是大作业水平的论文来“碰运气”，更有甚者，开启了“斐波那契”式投稿的恶劣风气，只期望能够有审稿人网开一面或者判断错误将自己的论文接收。这些浮躁功利的风气实在是令人不适，我强烈反对这类行为。

我对这篇论文的看法：我对这篇工作还是比较满意的，至少整个故事有理也有据，达到了让我满意的程度，我个人认为这不是一篇所谓水文（我永远不希望自己写出水文，更不会因为这是第一篇就放低自己的要求）。

最后，欢迎指正文章中的错误！arXiv 地址：https://arxiv.org/abs/2510.09001，论文代码会在投稿结束后再公开。

总结 科研