A Summary and Showcase of My First Research Project
Translated by Gemini 2.5 Pro. See original post here.
It’s been a little over a week since this project concluded, and actually, it’s my terminal procrastination that dragged it out until now I’ve decided to write an article to document this research journey. Technically, this might not be my first. I’ve worked in labs before, but for various reasons, those experiences didn’t lead to any significant output, let alone a first-author publication. Therefore, I don’t really count them as my “first research project.” I’d like to briefly share some of my thoughts on aspects like the idea and the writing process. Some of these may be naive or even incorrect, and I welcome any corrections in the comments.
Background
I’ve always been very interested in the RL + LLM area, or more specifically, RLVR (Reinforcement Learning from Verifiable Reward) not at all because this area has more mathematical formulas than other “filler” research directions. So, I chose this direction when I was initially picking a topic. By the time I started looking into this field (late May to early June), I had already discovered that RL for text-based reasoning was an incredibly competitive area. Simple ideas were no longer enough to guarantee a publication. Consequently, my senior colleague and I were in a constant state of anxiety throughout the project, worried that our idea might get scooped by another group at any moment.
I have to mention that before starting this journey, I had read the famous DAPO paper and was captivated by several of its elegant and obviously effective tricks. This sparked the idea of surpassing DAPO (which is also why we chose DAPO as one of our baselines). Later on, DAPO also provided the initial inspiration for our analysis and the proposal of a unified loss framework.
Additionally, my collaborator, TheRoadQAQ, was the nicest of the nice. Not only has he worked on RLVR for text and knows the field inside out, but he also carried me through the entire process, from the initial idea discussions and dataset selection to the final writing. It’s safe to say that this work wouldn’t have been completed without him. A huge thanks to him for his immense help 🙏.
The Idea
Initially, we hoped to use curriculum learning to accelerate the convergence speed of RL training, with the ultimate goal of reducing the required training time. This involved difficulty estimation and fewer rollout iterations. My senior colleague and I first thought of achieving more efficient learning by repeatedly sampling within the same batch based on difficulty. At that time, some works, like the aforementioned DAPO and https://arxiv.org/pdf/2504.03380, suggested that training models on medium-difficulty problems yielded greater improvements. Therefore, we used a Gaussian distribution with a mean of 0.5 (on a difficulty scale of ) and a standard deviation of 0.1 for sampling. The mean ensured that medium-difficulty problems had the highest probability of being sampled, while the variance, guided by the rule, ensured that the sampled problems’ difficulties were concentrated between , effectively filtering out samples that were too easy or too hard. As training progressed, the set of medium-difficulty problems would also change, thus automatically achieving the goal of curriculum learning.
Preliminary results showed that this sampling strategy was effective. However, its performance was similar to DAPO’s when we changed the dataset or model, and in some cases, it was even worse than the original GRPO. Furthermore, in the later stages of training, as the model’s capability significantly improved, the dataset consisted mostly of samples that were either completely unsolvable or always correct. This led to excessive resampling of the few moderately difficult samples, making the training highly prone to collapse. To analyze this collapse, I considered it from the perspective of sample advantage (adv). I realized that the so-called repeated sampling was merely multiplying the advantage by a coefficient (hereafter referred to as a weight). The original adv in GRPO is:
For a sample that has been repeatedly sampled times, its adv becomes:
This means . This implies that the final adv is a discrete weighted form of the original adv, with weights being . Such a manually defined and randomly obtained weighting scheme is highly unlikely to be the optimal one. Therefore, we shifted our focus to designing an optimal weight to improve the utilization of each sample and thus accelerate convergence.
Obviously, the optimal weight would be influenced by multiple factors, including model capability, dataset, training stage, and so on, making it nearly impossible to be manually designed. We concluded that such an optimal weight must be learned by the model itself, not handcrafted by humans. So, our idea evolved into assigning a learnable weight to each sample, which would be updated simultaneously during backpropagation, in an attempt to find the optimal weights. In fact, similar ideas have appeared in other papers, for instance, using classic methods like UCB to learn an appropriate weight. We felt these methods still had a degree of human design, which we wanted to avoid. We hoped the weights could be learned entirely by the model itself.
The idea was appealing, but practical training inevitably ran into problems. The most severe issue was that in a single complete training run, each sample might be trained on only a handful of times. For example, with 500 training steps, a batch size of 128, and a dataset of 45k samples, each sample would be used on average only times. In the worst-case scenario, a sample might be “seen” by the model only once, making it almost impossible to learn an optimal weight for it. On the other hand, from a theoretical standpoint, simply assigning a weight to each sample is not enough. The model might learn “tricks” to reduce the loss (a phenomenon we call “weight hacking”). For example, if all losses are positive, the model could just learn to set every weight to -inf to minimize the loss. Thus, our line of thought was again interrupted.
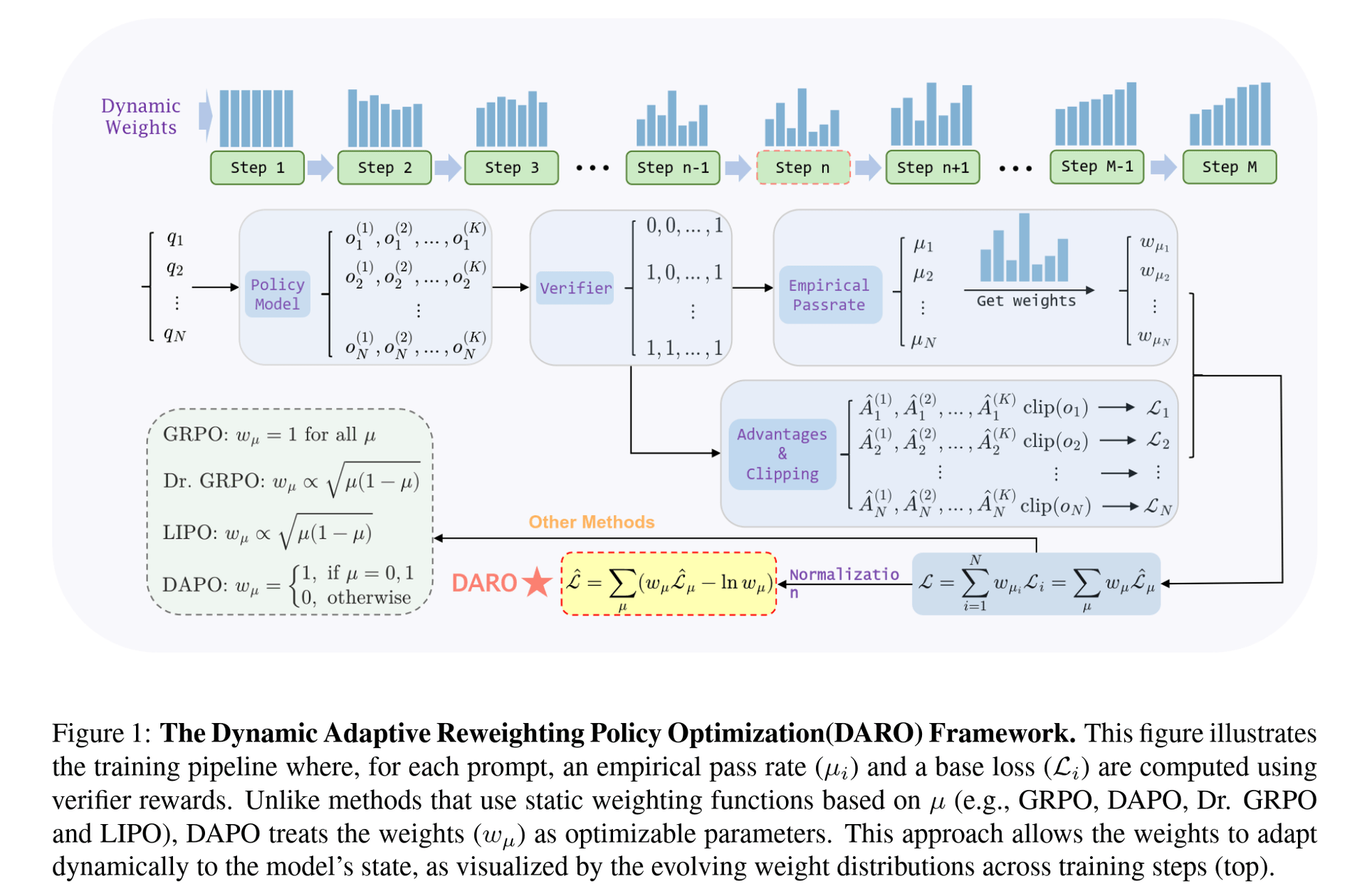
Since setting an individual weight for each sample was impractical, was there a compromise? Could we use some inherent properties of the samples to classify them and then apply weights at a group level? This is when we turned our attention back to DAPO. In DAPO, samples with a difficulty of 0 or 1 are completely discarded. In their code implementation, this is reflected by filtering out samples with an average reward (i.e., the pass rate of the sample during rollouts, which we’ll refer to as pass rate from now on) of 0 or 1. This gave us an idea: for each batch, after the rollouts are complete and rewards are calculated, we can group the samples by their pass rate! If there are rollouts in total, we can classify samples into groups with pass rates of . This would only require introducing a tensor of shape (K+1,) to achieve the weighting effect. This brought several benefits:
- In almost every step, samples with all possible pass rates would appear, allowing their corresponding weights to be continuously updated. This cleverly circumvented the major problem we mentioned earlier.
- Implementing this weighting only requires a tensor of length , which is independent of the data and the model, adding almost no extra computational or storage overhead.
- By allowing the model to learn the weights autonomously, we can implicitly achieve curriculum learning and improve training efficiency.
Now, only one problem remained: the “weight hacking” issue mentioned above. This was relatively easy to solve by adding a penalty term. Let the loss for a pass rate be , its weight be , and the penalty term be . The final loss function takes the form:
How do we derive this penalty term ? We wanted this term to be well-justified, not just picked by trying a few common terms and choosing the best one. Noticing that this term would also affect the final convergence state, we decided to go back to the beginning and analyze the GRPO loss, i.e., the properties of . We can derive that when using token-mean to aggregate the loss (we use this method because experiments in Lite PPO showed it performs better), the GRPO loss can be expressed as:
where is the dataset, are the model parameters, is the sum of response lengths, and is an abstraction of the adv-clip process. For a detailed derivation, please see our paper at https://arxiv.org/abs/2510.09001. Building on this, and combined with Hoeffding’s inequality, we can derive that in a single training step, can be approximated by the following equation:
Our experimental results show that this is an excellent approximation, as can be seen in Figure 2 of our paper, shown below:
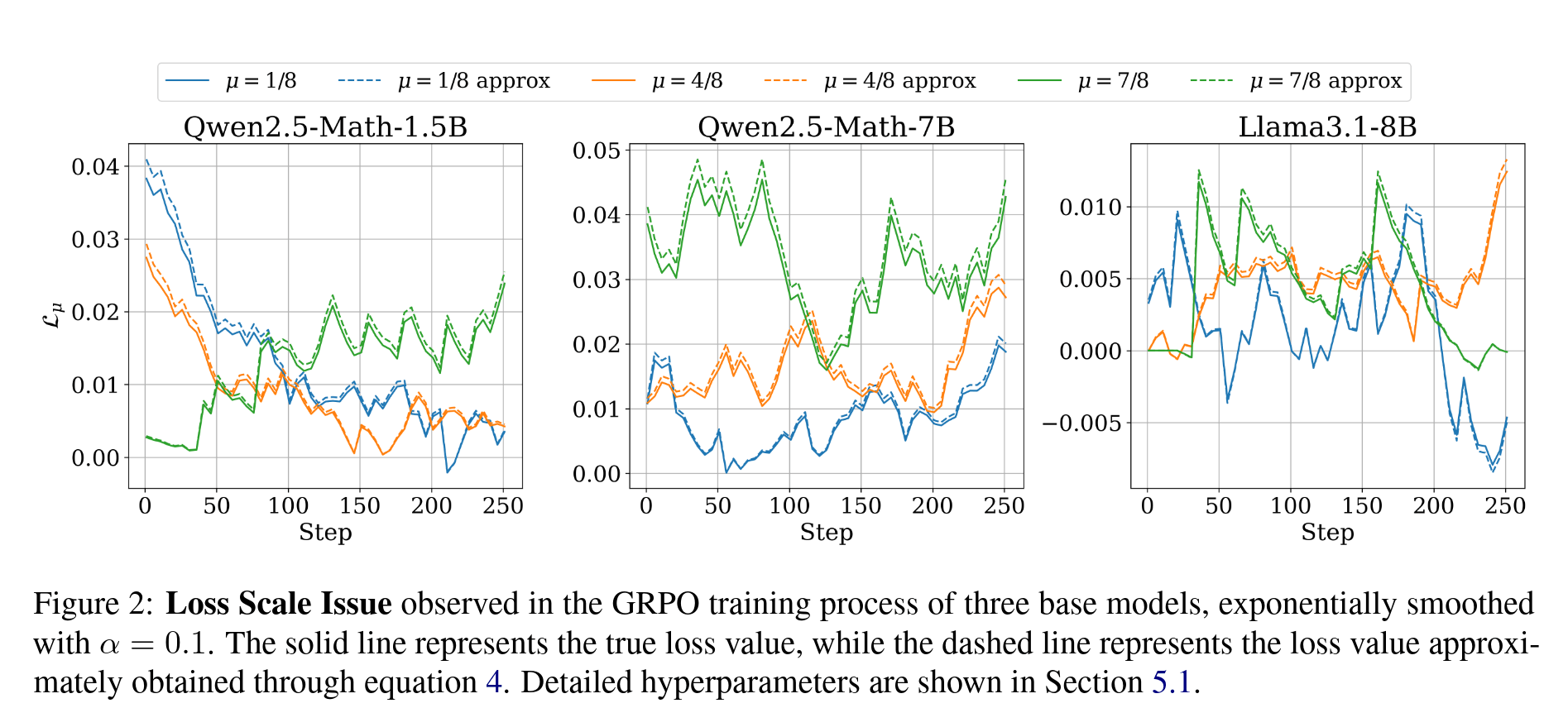
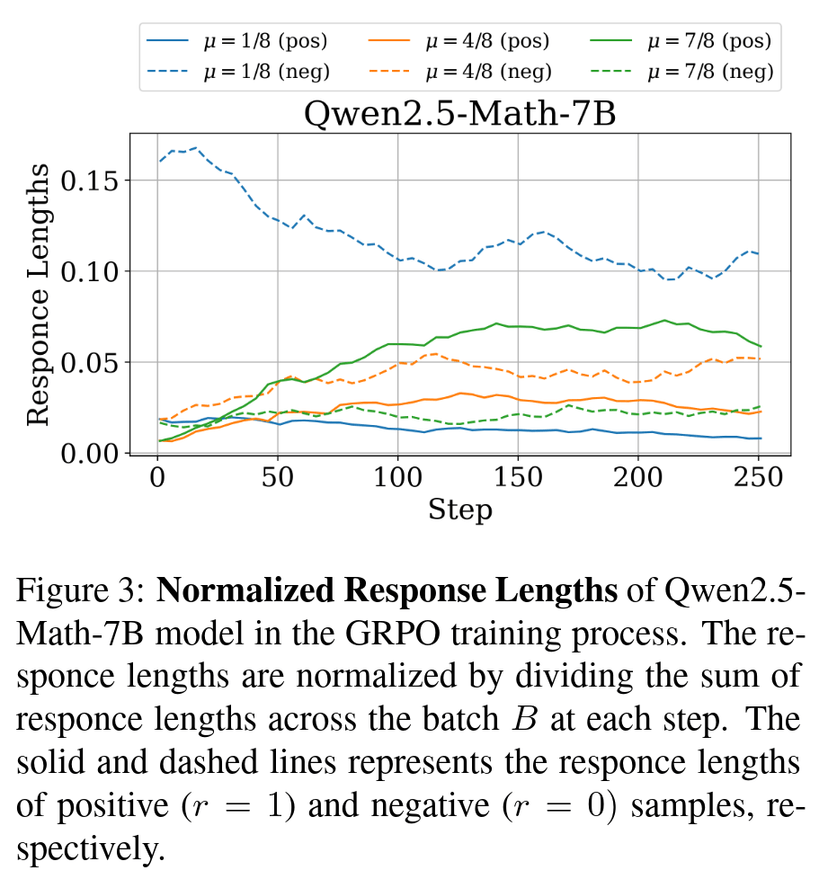
From this figure, we can also easily observe that the magnitude of is related to the model, the training progress, and most importantly, . The approximation also supports this conclusion, as it involves and the response length, the latter of which has been mentioned in several works (like Lite PPO) to be closely related to . We also conducted corresponding experiments to verify this conclusion, as shown in Figure 3 of our paper and Figure 6 in the appendix.
It is then evident that in the GRPO algorithm, the loss value changes with . Further observation of Figure 2 reveals that there will always be some or one for which the corresponding will dominate. This would cause the model to focus excessively on samples of a certain difficulty, which is clearly undesirable and likely to reduce training efficiency. Thus, how to set the penalty term became clear: we need this penalty term to, at convergence, make the model focus uniformly on samples of every difficulty level. In formulaic terms, this means , independent of . To maintain the freedom of weight learning, we set this as the final convergence condition, from which we can solve for the desired penalty term . Taking the partial derivative of the loss with respect to , we get:
Substituting allows us to solve for . Also recalling the data filtering operation in DAPO, which removes samples with , we arrive at the final form of the loss:

At this point, the core idea is essentially complete. See Algorithm 1 for the specific algorithm. What remains is our proposal of a unified framework for several RLVR algorithms. I will only present the conclusion here; for detailed derivations, please see our paper: https://arxiv.org/abs/2510.09001. We can unify GRPO, DAPO, Lite PPO, and our Dr.GRPO into the following form:
Where the expression for the weight is as follows:
| Algorithm | Weight |
|---|---|
| GRPO | |
| DAPO | |
| Lite PPO | |
| Dr.GRPO |
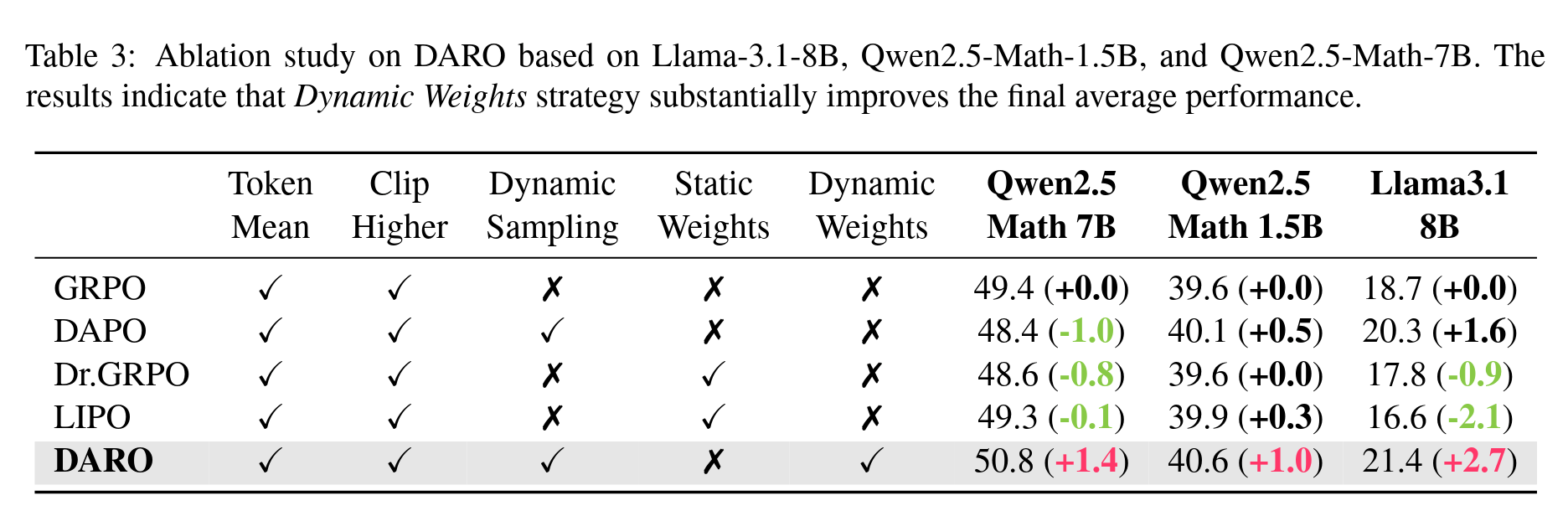
As can be seen, these methods are essentially simple weighting schemes for GRPO and are unlikely to be the optimal weighting method. The superiority of our DARO method is most evident here. For a more detailed analysis, please also refer to the paper. Here are some more result figures:
Some Result Figures and Tables
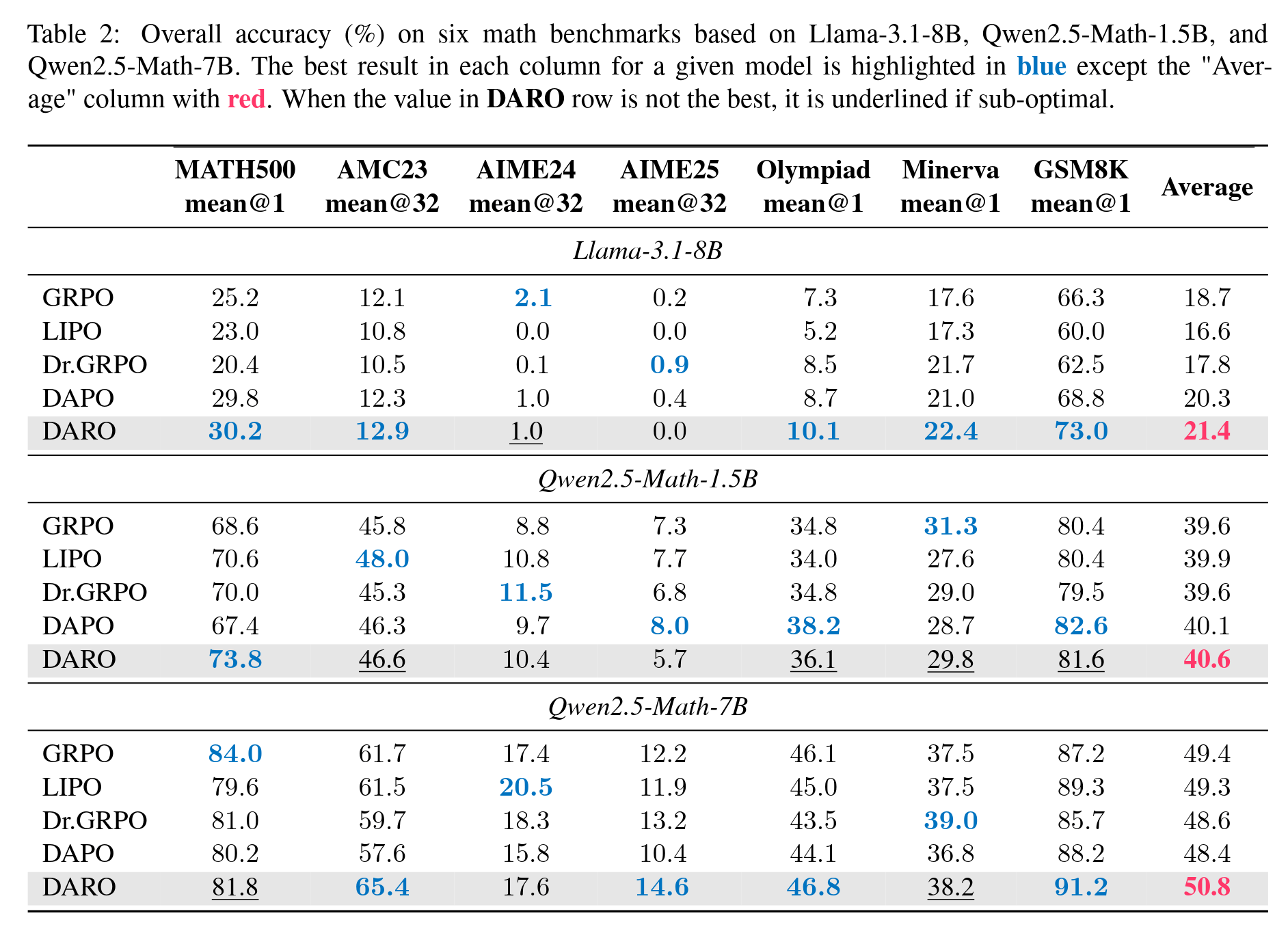
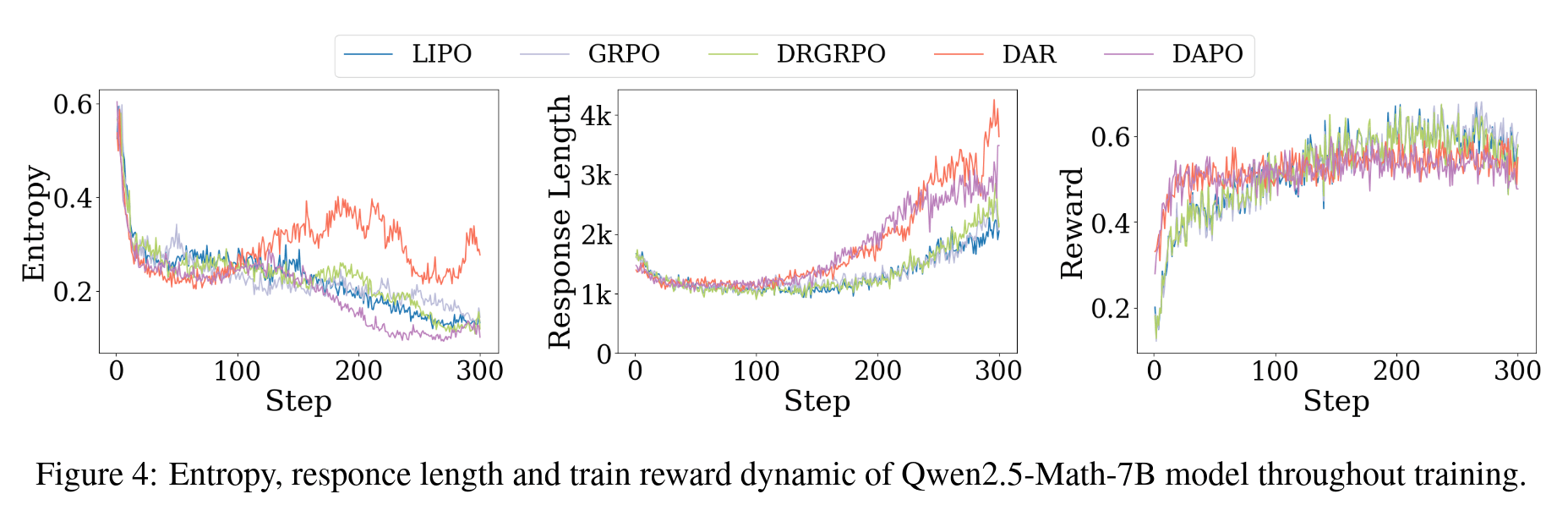
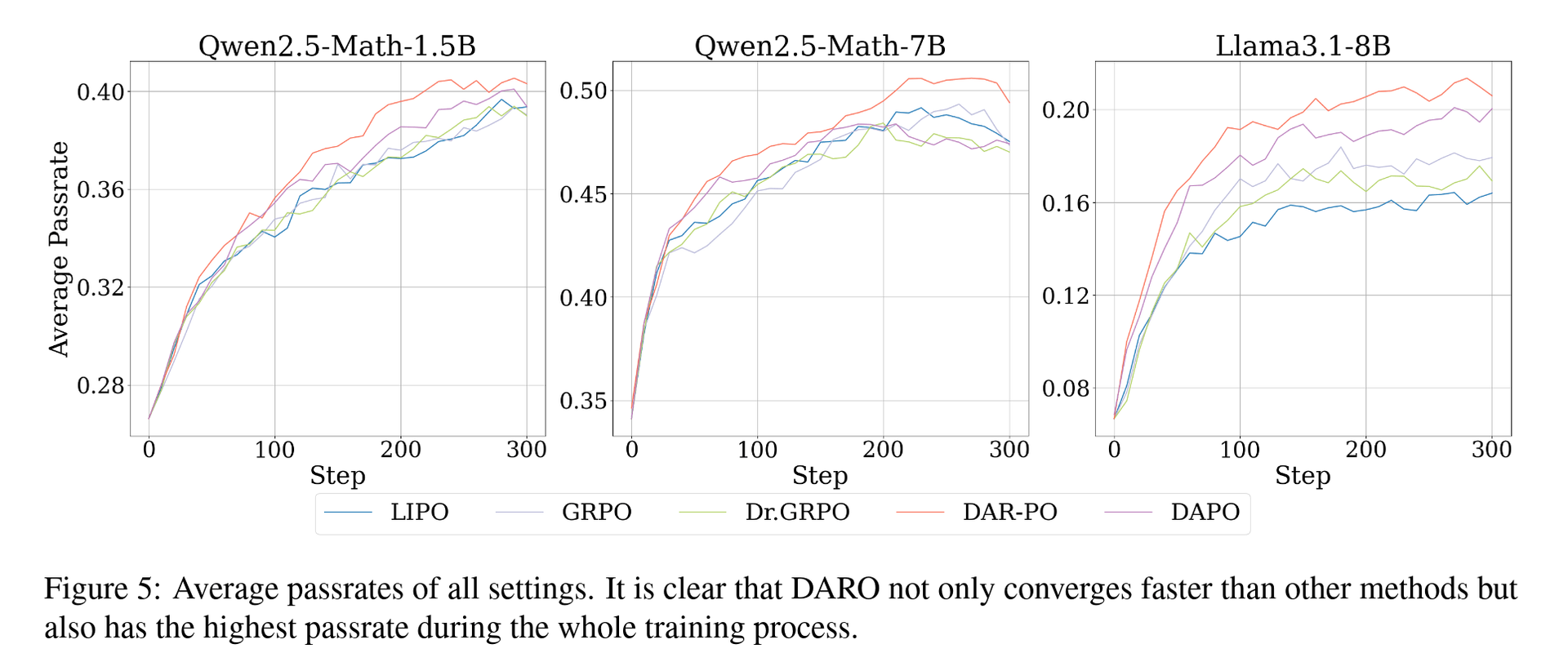
Writing
It turns out that my English writing skills are quite poor. I can’t even remember many common phrases used in papers, so writing directly in English was a real struggle for me. Therefore, I chose a relatively easier approach: first writing a rough draft in Chinese, then translating it into English for revisions, and finally, after the English version was complete, using AI for polishing. A key point to note is that during the polishing stage, you can ask the AI to explain the reasoning behind each change. This way, you can learn more “academic” expressions and also check if the AI’s modifications are correct.
I recommend watching the lecture on writing in GAMES003. It’s quite good. From my own experience, the main takeaways are:
- Writing needs a sense of “flow.” Each paragraph should have a central point and should focus on explaining that point well. Don’t cram too much into one paragraph. The points of different paragraphs can then be linked together to form a coherent story.
- Don’t write from the perspective of someone who ran the experiments. Instead, write from the perspective of the reader, showing them what the paper has done in a way that is most comfortable for them to understand (i.e., it should be very easy to grasp). I’m still not at this level yet 😢.
- The style of tables and figures throughout the paper needs to be consistent. It’s best to prepare a pleasant color scheme in advance.
- Use PPT for pipeline diagrams; it’s quite easy to get the hang of. Use matplotlib for other figures.
- Try to avoid having a tiny bit of text leftover at the end of a paragraph, as it can look unappealing.
- Writing it just once is definitely not enough. You need to spend at least a week revising it repeatedly.
I’m really not good at writing, and the paper only came together thanks to my senior colleague’s massive help. So grateful 😭.
Others
Beyond the paper, I have some other incomplete thoughts that I’ll briefly note down below.
On Choosing a Research Direction: I personally feel that the current field of large models is incredibly competitive. Entering a field too late inevitably presents many difficulties, for example:
- Too many different algorithms have been proposed for text-based reasoning, and most of the low-hanging fruit has been picked. The difficulty of proposing new and useful ideas has inevitably increased.
- Entering late means facing different treatment when submitting papers compared to what was hot at the time. Reviewers get tired of seeing the same things. If you’re late to the party, you’re bound to suffer from this debuff. For instance, the acceptance rate for speculative decoding at NeurIPS this year was quite worrying.
- If you enter late, everyone is basically chasing leaderboard scores. Even if your method is useful and novel, if it can’t beat other algorithms in terms of scores, it will naturally be looked down upon.
Of course, entering a field early also has its own pros and cons, which I won’t list here. I don’t have a good strategy for balancing this, as I’m still just a small fish in this big pond and can’t see the whole picture.
On Experiments: You must tune hyperparameters at the beginning! Tune them extensively to find a set of parameters that works well on all models and datasets before running the full-scale experiments. Although tuning takes time, it can greatly prevent situations where one set of parameters works for one model but causes another to collapse.
On Submission Volume: The number of submissions to major conferences has surged this year. A big reason for this is that too many people have entered the field, submitting papers that are at the level of a class project to “try their luck.” Even worse, some have started the惡劣 practice of “Fibonacci-style” submissions, just hoping that some reviewer will be lenient or make a mistake and accept their paper. This kind of impetuous and utilitarian atmosphere is really unpleasant, and I strongly oppose such behavior.
My Thoughts on This Paper: I am quite satisfied with this work. At least the whole story is logical and well-supported, reaching a level that I am happy with. I personally don’t consider this a so-called “filler” paper (I never want to write a filler paper, and I wouldn’t lower my standards just because it’s my first one).
Finally, please feel free to point out any errors in the article! arXiv link: https://arxiv.org/abs/2510.09001. The code for the paper will be released after the submission process is complete.
